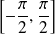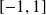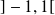Fonctions circulaires et réciproques.
Les fonctions sinus et cosinus peuvent être définies de diverses manières : géométriquement ou comme solutions d'une équation différentielle ou comme sommes de séries entières.
Fondamental :
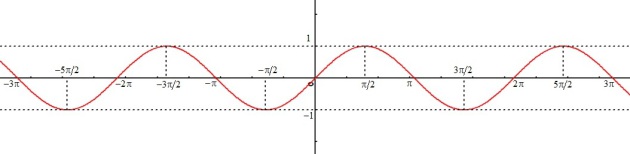
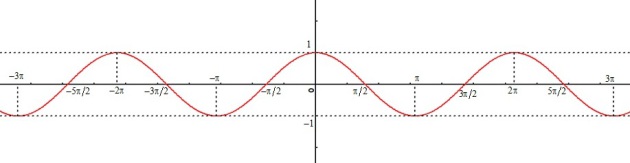
Fonction sinus
La fonction sinus est définie sur
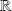, impaire et périodique de période
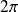.La fonction sinus est continue et indéfiniment dérivable sur
.
.
|  |
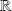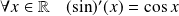Fondamental :
Fonction cosinus
La fonction cosinus est définie sur
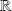, paire et périodique de période
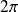.La fonction cosinus est continue et indéfiniment dérivable sur
.
.
|  |
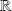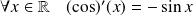Fondamental :
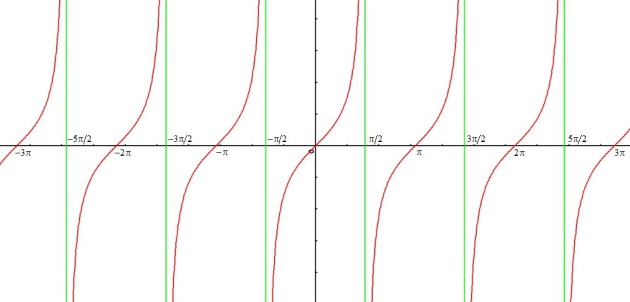
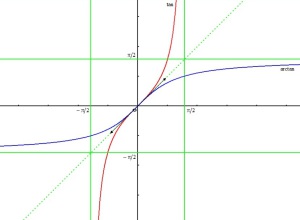
Fonction tangente
La fonction tangente est définie sur
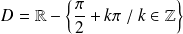par :
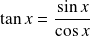.La fonction tangente est impaire et périodique de période
.
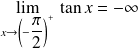et
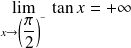.La fonction tangente est continue et indéfiniment dérivable sur son ensemble de définition.
.
|  |
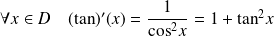Fondamental :
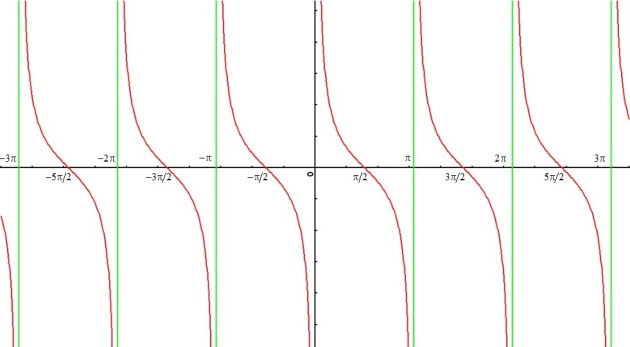
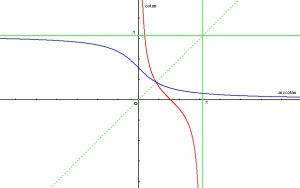
Fonction cotangente
La fonction cotangente est définie sur
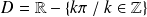par :
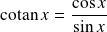.La fonction cotangente est impaire et périodique de période
.
et
.La fonction cotangente est continue et indéfiniment dérivable sur son ensemble de définition.
.
|  |
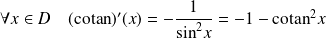