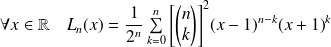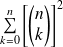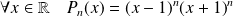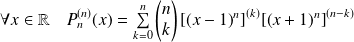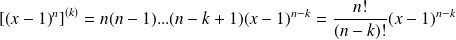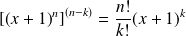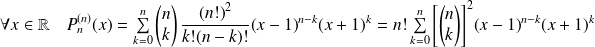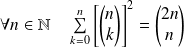Exo 17
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Pour tout entier naturel
, on considère le polynôme défini par :
.
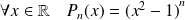On lui associe le polynôme
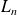défini par :
.
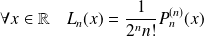Question
Pour tout entier
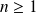, déterminer le degré du polynôme
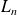et calculer son coefficient dominant.
Déterminez le degré et le coefficient dominant de la dérivée d'ordre
de
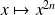, puis de
.
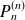Le polynôme
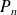est de degré
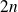, donc sa dérivée d'ordre
est un polynôme de degré
.
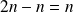Donc
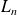est un polynôme de degré
.
Le coefficient dominant de
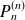est le coefficient dominant de la dérivée d'ordre
de
.
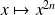Donc le coefficient dominant de
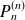est :
.
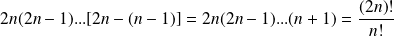Or :
.
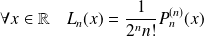Conclusion : Le coefficient dominant de
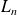est
.
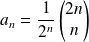Question
Démontrer que le polynôme
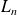admet
racines réelles distinctes dans l'intervalle
.
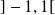Déterminez le nombre de racines des dérivées
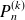en utilisant le théorème de Rolle.
.
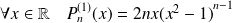Donc
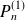est un polynôme de degré
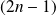qui admet une racine simple
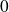et deux racines
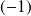et
d'ordre
.
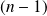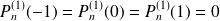et
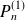est continue et dérivable sur
.
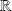Donc d'après le théorème de Rolle, il existe
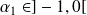et
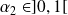tels que
.
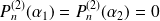Or :
.
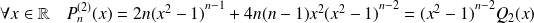Donc
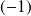et
sont racines d'ordre
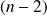du polynôme
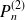qui est de degré
.
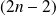Donc
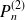admet deux racines simples
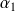et
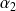dans
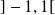, et deux racines
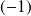et
d'ordre
.
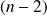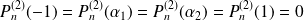. On applique le théorème de Rolle.
Il existe
,
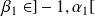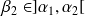et
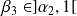tels que :
.
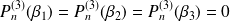Et :
.
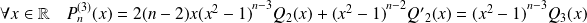Donc
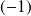et
sont racines d'ordre
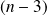du polynôme
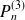qui est de degré
.
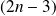Donc
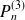admet trois racines simples
,
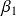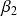et
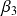distinctes dans
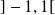, et deux racines
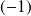et
d'ordre
.
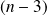On continue ce raisonnement jusqu'à l'ordre
.
Donc
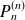est un polynôme de degré
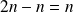qui admet
racines réelles distinctes dans
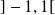(et donc pas d'autres racines).
Conclusion : Le polynôme
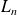admet
racines réelles distinctes dans
.
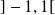Question
Question
Vérifier que :
.
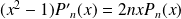En déduire que :
.
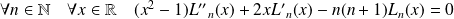Dérivez
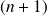fois la relation avec la formule de Leibniz.
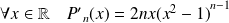, donc :
.
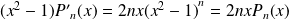On dérive
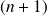fois cette relation avec la formule de Leibniz.
Donc :
.
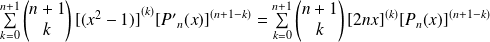Dans la première somme, les termes sont nuls pour
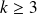et dans la deuxième pour
.
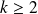Donc :
.
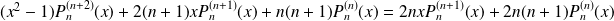Donc :
.
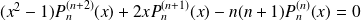Or :
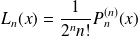, donc :
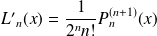et :
.
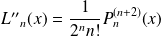Conclusion :
.
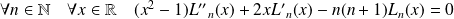Question
Exprimer
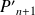et
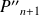en fonction de
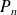et
.
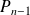En déduire que :
.
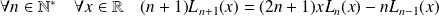Utilisez la formule de Leibniz pour obtenir deux expressions de
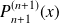, puis éliminez
.
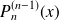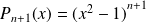, donc :
.
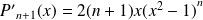Conclusion :
.
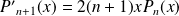Et :
.
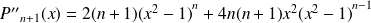Donc :
.
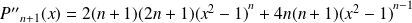Conclusion :
.
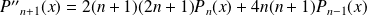On dérive
fois la première relation :
.
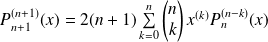Donc :
.
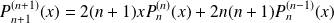On dérive
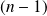fois la deuxième relation :
.
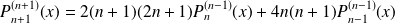On combine les deux égalités pour éliminer
.
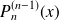Donc :
.
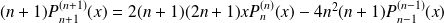On divise par
.
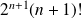Conclusion :
.
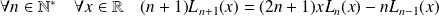