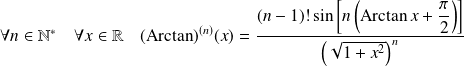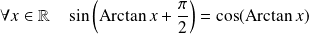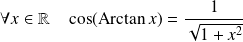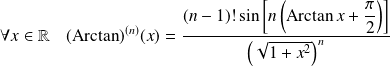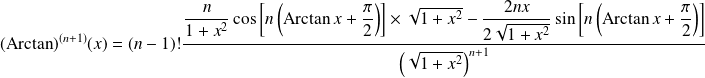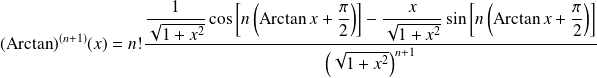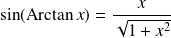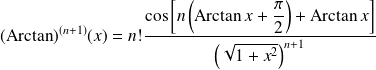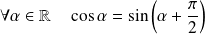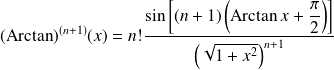Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Démontrer que, pour tout entier
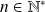, il existe un polynôme
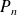tel que :
.
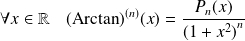Raisonnez par récurrence.
On raisonne par récurrence.
Initialisation :
.
Donc il existe un polynôme
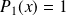tel que :
.
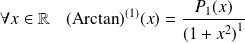Hérédité : Soit un entier
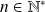pour lequel il existe un polynôme
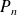tel que :
.
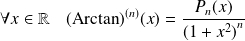Donc :
.
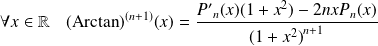Donc :
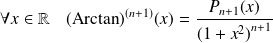en posant :
.
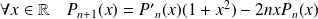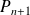est un polynôme comme somme et produit de polynômes.
Conclusion : Pour tout entier
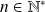, il existe un polynôme
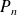tel que
.
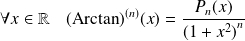Question
Déterminer le coefficient dominant du polynôme
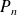et son degré.
Examinez les premiers termes, conjecturez le résultat et démontrez le par récurrence.
On examine les premiers termes :
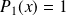, donc :
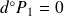et le coefficient dominant est :
.
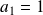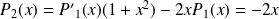, donc :
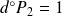et le coefficient dominant est :
.
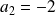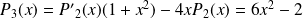, donc :
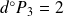et le coefficient dominant est :
.
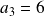On conjecture que :
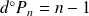et que le coefficient dominant est :
.
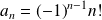On le démontre par récurrence.
Initialisation : Elle est déjà faite pour
,
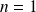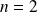et
.
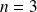Hérédité : Soit un entier
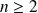tel que :
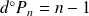et tel que le coefficient dominant de
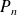soit :
.
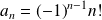Donc :
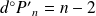et le coefficient dominant de
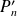est :
.
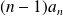On a vu que :
.
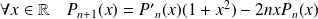Or :
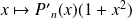est un polynôme de degré
et de coefficient dominant
.
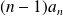Et :
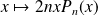est un polynôme de degré
et de coefficient dominant
.
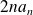Donc
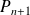est un polynôme de degré
et de coefficient dominant :
.
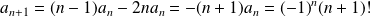Conclusion : Pour tout
,
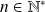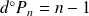et son coefficient dominant est
.
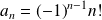Question
Question
En déduire la factorisation du polynôme
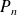pour tout entier
.
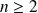Déterminez les racines du polynôme
.
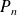On a vu que :
.
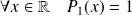Et :
.
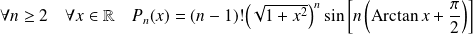Donc les racines de
sont les solutions de l'équation :
.
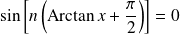Elles vérifient donc :
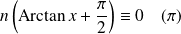, donc :
.
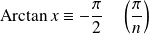Donc :
. Or :
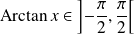, donc :
.
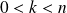Les racines de
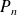sont donc les réels :
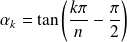pour
.
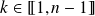Le polynôme
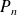a donc
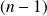racines réelles :
pour
.
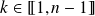Il est de degré
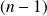et de coefficient dominant :
.
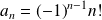Conclusion :
.
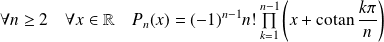