Solution

Il s'agit de montrer que : .

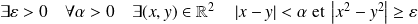Par symétrie entre et , et 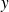par parité de la fonction, on peut prendre : .

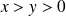Et on suppose : 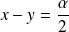pour avoir : .

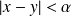Donc : .

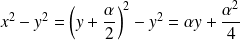Donc pour que 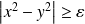, il suffit que : 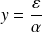et donc : .

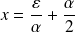Par exemple, pour : .

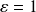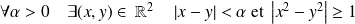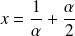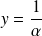Il suffit de prendre : et car : .

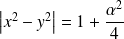Conclusion : La fonction 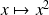est continue sur 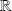mais pas uniformément continue.