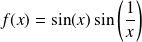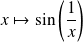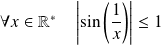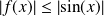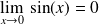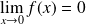Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Question
Etudier l'existence d'une limite en
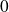de la fonction définie par :
.
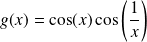Montrez qu'il existe deux suites qui convergent vers
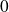, et dont les images par la fonction
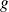ne convergent pas vers la même limite.
La fonction
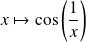n'admet pas non plus de limite en
.
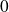Soit :
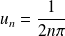et
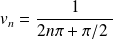pour tout entier naturel non nul
.
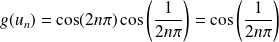. Donc :
.
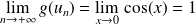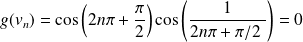. Donc :
.
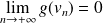On a donc trouvé deux suites
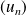et
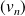qui convergent vers
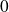, et dont les images par la fonction
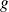ne convergent pas vers la même limite.
Conclusion : La fonction
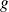n'admet pas de limite en
.
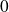