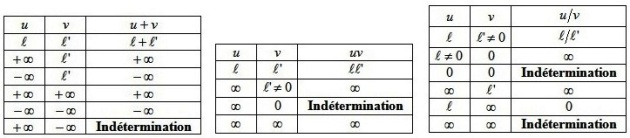
Propriétés des limites
Dans ce qui suit,
est réel ou infini, et les fonctions sont supposées définies au voisinage de
.
Fondamental :
Opérations algébriques :
Soient
et
deux fonctions numériques définies au voisinage de
.
Les tableaux suivants donnent les limites de leur somme, de leur produit et de leur quotient en fonction de leurs limites (
et
sont des réels).
Pour le produit et le quotient, on complète en étudiant le signe des fonctions
et
au voisinage de
.
Fondamental :
Composition (
,
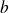et
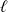sont réels ou infinis)
Si
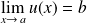et si
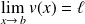, alors
.
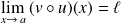En posant
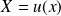, on obtient :
.
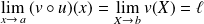Fondamental :
Compatibilité avec l'ordre (
est réel ou infini,
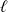et
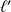sont réels)
Si
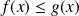pour tout
au voisinage de
et :
si
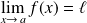et
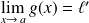, alors
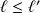(même si l'inégalité sur les fonctions est stricte).si
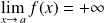, alors
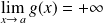.si
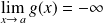, alors
.
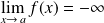Fondamental :
Théorème d'encadrement (
est réel ou infini)
Si
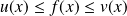pour tout
au voisinage de
, et si les deux fonctions
et
admettent en
la même limite réelle :
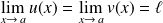, alors la fonction
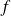admet en
une limite égale à
:
.
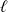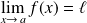Ce théorème ne donne pas seulement le calcul de la limite, mais prouve l'existence de la limite.
Fondamental :
Limite d'une fonction monotone
Si
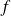est une fonction croissante sur
(
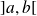et
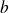sont réels ou infinis) :
Si
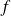est majorée, alors
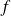a une limite réelle en
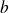. Et si
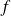n'est pas majorée :
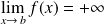.Si
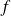est minorée, alors
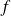a une limite réelle en
. Et si
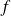n'est pas minorée :
.
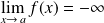Si
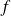est une fonction décroissante sur
(
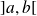et
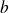sont réels ou infinis) :
Si
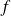est minorée, alors
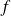a une limite réelle en
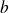. Et si
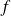n'est pas minorée :
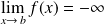.Si
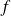est majorée, alors
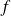a une limite réelle en
. Et si
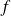n'est pas majorée :
.
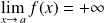Fondamental :
Caractérisation séquentielle d'une limite (
et
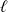sont réels ou infinis)
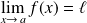si et seulement si, pour toute suite
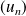convergeant vers
, la suite
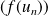converge vers
.
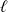Donc pour démontrer qu'une fonction
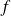n'admet pas la limite
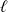, il suffit de trouver une suite
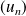convergeant vers
telle que la suite
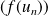ne converge pas vers
.
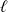Et pour démontrer qu'une fonction
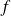n'admet pas de limite, il suffit de trouver deux suites
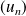et
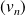convergeant vers
telles que les suites
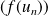et
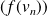n'admettent pas la même limite.
