Exo 17
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
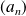une suite réelle, positive et bornée.
On considère la suite
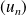définie par
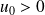et
.
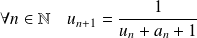Question
Montrer que la suite
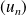converge si et seulement si la suite
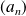converge.
Démontrez successivement les deux implications.
Si
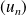converge, exprimez
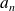en fonction de
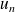et
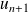pour montrer la convergence de
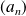.Si
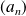converge, déterminez la seule limite possible
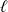de
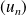, puis montrez que
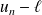tend vers
.
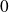Une récurrence évidente montre que :
.
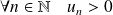On démontre successivement les deux implications.
On suppose que la suite
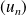converge. Soit :
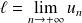et donc :
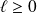.Si
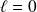, on aurait :
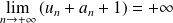, donc :
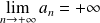.Or ceci n'est pas possible car la suite
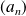est bornée. Donc :
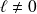. Or :
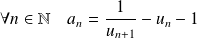. Donc la suite
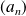converge vers
.
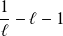On suppose que la suite
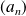converge. Soit :
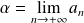et donc :
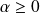.Si la suite
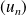converge, sa limite est solution de l'équation :
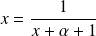, donc de l'équation :
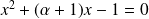. Le discriminant est :
(
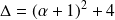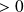). Donc l'équation a deux racines réelles distinctes.Ces deux racines sont de signes contraires car leur produit est
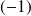.Or :
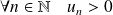. Donc si la suite
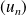converge, sa limite est la racine positive de l'équation. Montrons donc que
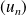converge vers :
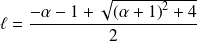.On a :
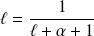. Donc :
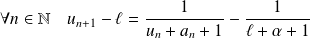.Donc :
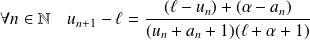.Donc :
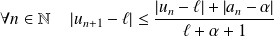car
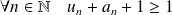.Or :
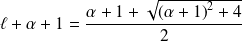, donc :
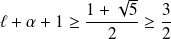.Donc :
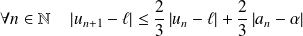.Donc :
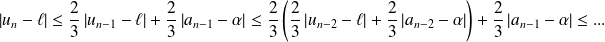.Donc par récurrence :
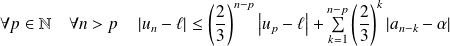.Soit
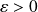. On sait que :
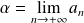. Donc :
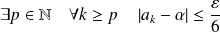.Or :
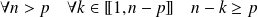donc :
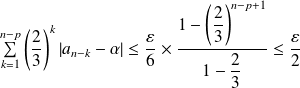.Et
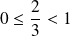, donc :
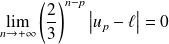, donc :
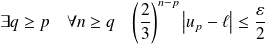.Donc :
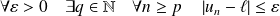. Donc la suite
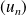converge vers
.
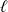Conclusion : La suite
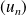converge si et seulement si la suite
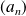converge.
