Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
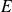un plan vectoriel euclidien orienté et
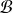une base orthonormale directe.
Soient
et
deux vecteurs non nuls tels que
.
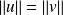Question
Démontrer qu'il existe un unique endomorphisme
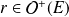tel que
.
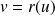Raisonnez sur les matrices.
Utilisez les complexes, par exemple, pour trouver la forme des matrices de
et de
.
Si
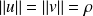, les vecteurs
et
ont pour affixes respectives
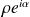et
.
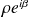Donc ils ont pour matrices respectives
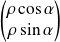et
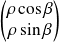dans la base
.
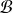Soit
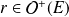. Donc
a une matrice dans
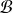de la forme :
.
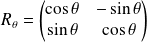Donc le vecteur
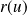a pour matrice :
.
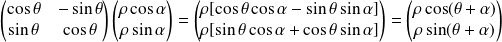Donc
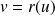si et seulement si :
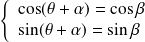, donc si :
.
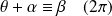Donc
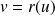si et seulement si
a pour matrice
.
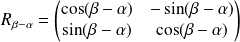Conclusion : Il existe un unique endomorphisme
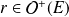tel que
.
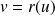Question
Démontrer qu'il existe un unique endomorphisme
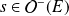tel que
.
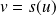Raisonnez sur les matrices.
Soit
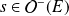. Donc
a une matrice dans
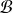de la forme :
.
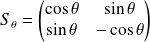Donc le vecteur
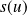a pour matrice :
.
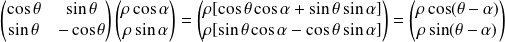Donc
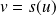si et seulement si :
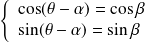, donc si :
.
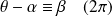Donc
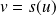si et seulement si
a pour matrice
.
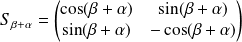Conclusion : Il existe un unique endomorphisme
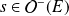tel que
.
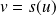