Groupe orthogonal en dimension 2
On suppose l'espace vectoriel euclidien
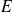orienté et rapporté à une base
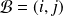orthonormale directe.
Fondamental :
Groupe orthogonal en dimension 2
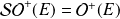est l'ensemble des endomorphismes dont la matrice dans la base
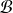est de la forme :
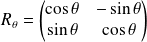où
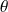est un réel.
est l'ensemble des endomorphismes dont la matrice dans la base
est de la forme :
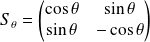où
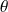est un réel.
Remarque :
En dimension
,
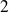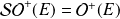est un groupe commutatif.En dimension
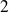, tous les éléments de
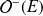sont des réflexions.
Fondamental :
Propriété :
Une rotation admet la même matrice dans n'importe quelle base orthonormale directe.
Conséquence : La classe d'équivalence modulo
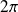de
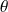est une caractéristique de la rotation.
Fondamental :
Classification par l'ensemble
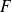des vecteurs invariants de l'endomorphisme
:
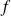Si
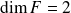, alors
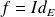.Si
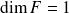, alors
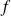est la réflexion par rapport à la droite
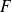.Si
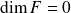, alors
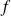est une rotation distincte de
.
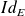