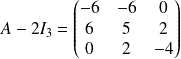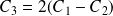Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
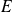un espace vectoriel de base
et
l'endomorphisme de
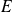de matrice
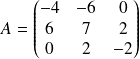dans la base
.
Question
Déterminer l'image par
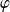du vecteur
.
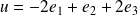Le vecteur
a pour matrice
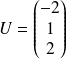, donc
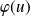a pour matrice
.
Conclusion :
.
Question
Déterminer le noyau de
.
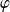Un vecteur
de matrice
appartient à
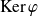si et seulement si
, donc si
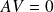, donc si
, donc si
.
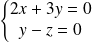Conclusion :
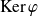est la droite vectorielle de base
.
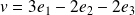Question
Question
Montrer que
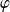est diagonalisable et déterminer une base de vecteurs propres.
Inutile de chercher le polynôme caractéristique !
Utilisez les questions précédentes.
Méthode :
En interprétant les résultats des questions précédentes, on évite le calcul du polynôme caractéristique.
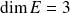, donc
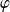a au plus
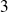valeurs propres.
Or d'après la première question,
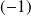est valeur propre de
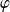et
est vecteur propre associé à la valeur propre
.
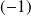D'après la deuxième question,
est valeur propre de
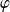et le sous-espace propre associé est
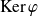, donc
est un vecteur propre associé à la valeur propre
.
D'après la troisième question,
est valeur propre de
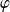, et les colonnes de
sont liées par la relation :
.
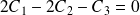Donc, si
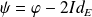, on a la relation
.
Donc le vecteur
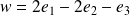vérifie :
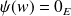, donc
.
Donc le vecteur
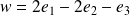est vecteur propre de
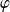associé à la valeur propre
.
Donc
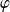a trois valeurs propres distinctes :
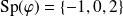et les sous-espaces propres sont donc de dimension
.
Conclusion :
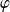est diagonalisable.
Une base de vecteurs propres est
,
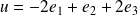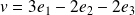et
.
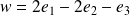