Diagonalisation
Dans ce qui suit,
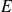 désigne un espace vectoriel de dimension
désigne un espace vectoriel de dimension
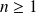 .
.
Définition :
Un endomorphisme
 est diagonalisable s'il existe une base de
est diagonalisable s'il existe une base de
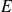 formée de vecteurs propres de
formée de vecteurs propres de
 .
.
Définition :
Une matrice
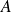 est diagonalisable si
est diagonalisable si
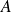 est semblable à une matrice diagonale : il existe une matrice inversible
est semblable à une matrice diagonale : il existe une matrice inversible
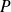 et une matrice diagonale
et une matrice diagonale
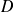 telles que
telles que
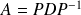 .
.
Fondamental :
Propriétés :
Une matrice
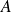 est diagonalisable si et seulement si l'endomorphisme
est diagonalisable si et seulement si l'endomorphisme
 associé l'est.
associé l'est.Un endomorphisme
 est diagonalisable si et seulement si
est diagonalisable si et seulement si
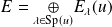 .
.Un endomorphisme
 est diagonalisable si et seulement si
est diagonalisable si et seulement si
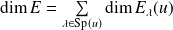 .
.Un endomorphisme
 est diagonalisable si et seulement si son polynôme caractéristique
est diagonalisable si et seulement si son polynôme caractéristique
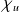 est scindé et si :
est scindé et si :
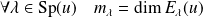 .
.Un endomorphisme
 est diagonalisable si et seulement si
est diagonalisable si et seulement si
 annule un polynôme scindé à racines simples.
annule un polynôme scindé à racines simples.Si
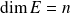 et si l'endomorphisme
et si l'endomorphisme
 a
a
 valeurs propres distinctes, alors
valeurs propres distinctes, alors
 est diagonalisable.
est diagonalisable.
Fondamental :
Décomposition spectrale :
Si un endomorphisme
 est diagonalisable et
est diagonalisable et
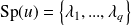 , alors
, alors
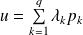 où
où
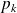 est le projecteur associé à
est le projecteur associé à
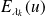 .
.





