Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère la matrice
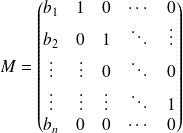 où
où
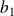 , ...,
, ...,
 sont des réels positifs ou nuls et
sont des réels positifs ou nuls et
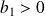 .
.
Question
Calculer son polynôme caractéristique.
Déterminez successivement un polynôme annulateur de la matrice, le polynôme minimal, puis le polynôme caractéristique.
Soit
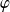 l'endomorphisme de
l'endomorphisme de
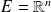 de matrice
de matrice
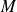 dans la base canonique
dans la base canonique
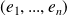 .
.
Donc :
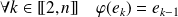 , et
, et
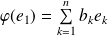 .
.
Donc :
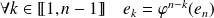 , et donc :
, et donc :
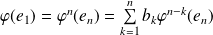 .
.
Donc :
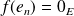 si
si
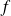 est l'endomorphisme :
est l'endomorphisme :
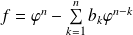 avec
avec
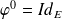 .
.
Et :
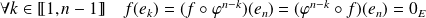 car
car
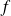 commute avec
commute avec
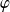 .
.
Donc l'endomorphisme
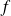 est nul. Donc le polynôme
est nul. Donc le polynôme
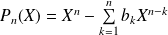 est un polynôme annulateur de
est un polynôme annulateur de
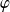 .
.
Donc le polynôme minimal
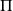 de
de
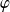 divise le polynôme
divise le polynôme
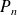 .
.
Soit
 le degré de
le degré de
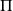 :
:
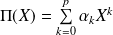 avec
avec
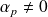 , et
, et
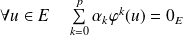 .
.
Donc :
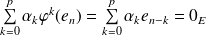 , donc, si
, donc, si
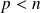 , la famille
, la famille
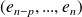 serait liée, ce qui est faux.
serait liée, ce qui est faux.
Donc le polynôme
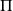 est de degré
est de degré
 et unitaire, donc
et unitaire, donc
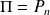 .
.
Or le polynôme minimal divise le polynôme caractéristique qui est lui aussi de degré
 , mais de coefficient dominant
, mais de coefficient dominant
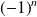 .
.
Donc
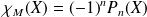 .
.
Conclusion : Le polynôme caractéristique de
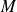 est
est
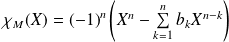 .
.
Remarque :
On aurait pu démontrer ce résultat par récurrence.
Question
Montrer que la matrice
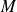 a une et une seule valeur propre strictement positive.
a une et une seule valeur propre strictement positive.
Raisonnez par récurrence.
Les valeurs propres de
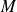 sont les racines de
sont les racines de
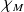 , donc de
, donc de
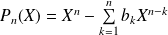 .
.
Montrons par récurrence que, pour tout entier
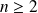 , tout polynôme de la forme
, tout polynôme de la forme
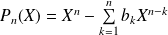 (avec
(avec
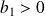 et
et
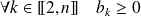 ) possède une et une seule racine dans
) possède une et une seule racine dans
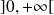 .
.
Initialisation :
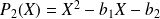 a pour discriminant
a pour discriminant
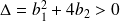 , donc, si
, donc, si
 , il a deux racines de signes contraires, et si
, il a deux racines de signes contraires, et si
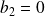 , les racines sont
, les racines sont
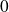 et
et
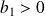 .
.
Donc dans les deux cas,
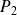 a une et une seule racine strictement positive.
a une et une seule racine strictement positive.
Hérédité : Soit
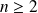 tel que tout polynôme de la forme
tel que tout polynôme de la forme
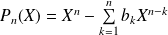 (avec
(avec
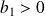 et
et
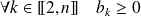 ) possède une et une seule racine dans
) possède une et une seule racine dans
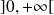 .
.
Soit
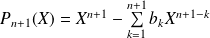 avec
avec
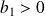 et
et
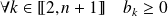 .
.
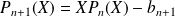 où
où
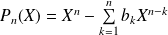 avec
avec
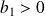 et
et
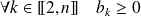 .
.
Si
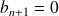 ,
,
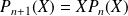 possède une seule racine dans
possède une seule racine dans
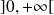 qui est celle de
qui est celle de
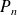 .
.
Si
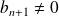 ,
,
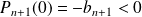 et
et
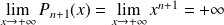 .
.
Donc le polynôme
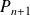 s'annule au moins une fois sur
s'annule au moins une fois sur
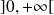 .
.
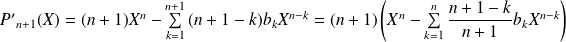 .
.
Or
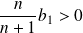 et
et
 .
.
Donc d'après l'hypothèse de récurrence, le polynôme
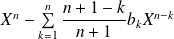 a une et une seule racine
a une et une seule racine
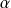 dans
dans
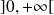 . Donc
. Donc
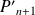 a une seule racine
a une seule racine
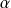 dans
dans
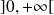 .
.
Or
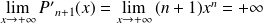 , donc
, donc
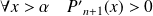 .
.
Donc, il y a deux possibilités :
Or
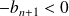 , donc dans les deux cas,
, donc dans les deux cas,
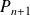 s'annule une seule fois dans
s'annule une seule fois dans
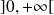 .
.
Conclusion : Pour tout entier
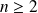 , le polynôme
, le polynôme
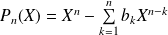 (avec
(avec
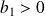 et
et
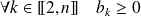 ) possède une et une seule racine dans
) possède une et une seule racine dans
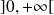 .
.
Conclusion : La matrice
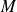 a une et une seule valeur propre strictement positive.
a une et une seule valeur propre strictement positive.






