Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
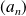 une suite de réels.
une suite de réels.
Question
Déterminer les valeurs propres de la matrice
 pour
pour
 .
.
Déterminez par récurrence le polynôme caractéristique de la matrice.
Soit
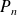 le polynôme caractéristique de la matrice
le polynôme caractéristique de la matrice
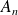 :
:
 .
.
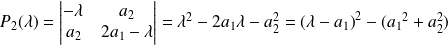 .
.
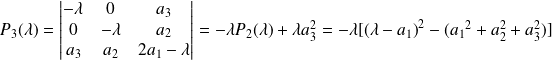 .
.
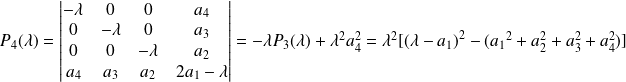 .
.
Montrons par récurrence que :
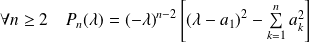 .
.
Initialisation : Elle est déjà faite.
Hérédité : Soit
 tel que
tel que
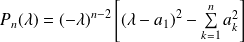 .
.
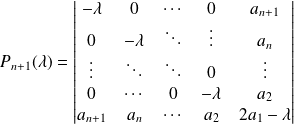 . On développe suivant la première colonne.
. On développe suivant la première colonne.
 .
.
Donc :
 .
.
Donc :
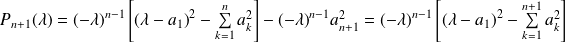 .
.
Conclusion :
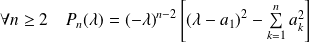 .
.
Conclusion :
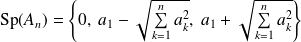 si
si
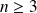 , et
, et
 .
.
Question
En déduire que le rang de
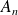 .
.
Le rang dépend de la dimension du noyau, sous-espace propre associé à la valeur propre 0.
Si
 , alors
, alors
 , donc
, donc
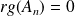 .
.
Si
 et
et
 , alors
, alors
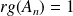 .
.
Sinon,
 , donc
, donc
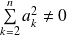 , donc
, donc
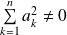 et
et
 .
.
Donc les trois valeurs propres
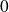 ,
,
 et
et
 sont distinctes.
sont distinctes.
Donc les sous-espaces propres sont en somme directe. Or
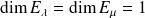 , donc
, donc
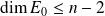 .
.
Or
 . Donc
. Donc
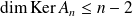 , donc
, donc
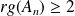 .
.
Si
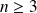 , tous les déterminants extraits d'ordre
, tous les déterminants extraits d'ordre
 sont nuls car ils sont tous de la forme
sont nuls car ils sont tous de la forme
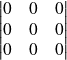 , ou
, ou
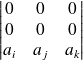 , ou
, ou
 , ou
, ou
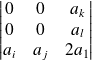 . Donc
. Donc
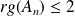 .
.
Conclusion :
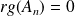 si
si
 .
. 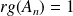 si
si
 et
et
 .
. dans les autres cas.
dans les autres cas.





