Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit un entier
et
l'application qui, à tout polynôme
de
, associe le polynôme :
.
Question
Montrer que
est un endomorphisme de
.
Montrez que
est linéaire et que
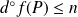pour tout polynôme
de
.
Soit
et
deux polynômes de
, et
un réel.
.
Donc :
.
Donc :
.
Donc :
. Donc
est linéaire.
Si
et
, alors
avec
et
avec
.
Donc :
.
et le coefficient de
est
.
et le coefficient de
est
.
Donc
et le coefficient de
est
.
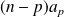Donc, si
, alors
et si
, alors
.
Or
. Donc dans tous les cas
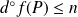. Donc
.
Conclusion :
est un endomorphisme de
.
Question
Montrer que si
est un vecteur propre de
, alors
.
Si
est vecteur propre de
,
et il existe
tel que
.
Soit
. On a vu que si
,
. Or
si
et
si
. Donc
n'est jamais égal à
si
, et donc
.
Conclusion : Si
est un vecteur propre de
, alors
.
Question
Montrer que si
est un vecteur propre de
, ses racines appartiennent à
.
Soit
un vecteur propre de
. Donc
,
et il existe
tel que
.
Donc :
.
Donc :
. Notons
cette relation.
Soit
une racine de
et
son ordre de multiplicité.
Donc il existe un polynôme
tel que
avec
.
Donc :
.
Donc, d'après (
) :
.
Donc :
. Donc :
.
Conclusion : Si
est un vecteur propre de
, ses racines appartiennent à
.
Question
En déduire les valeurs propres et les vecteurs propres de
.
Soit
un vecteur propre de
. Donc
et il existe
tel que
.
Son degré est
et ses racines appartiennent à
.
Donc le polynôme est de la forme :
où
et
.
Donc :
.
Donc :
.
Donc :
.
Donc :
. Donc :
.
Donc, si
,
est un vecteur propre associé à la valeur propre
.
On obtient ainsi
valeurs propres distinctes. Or
.
Donc
n'a pas d'autre valeur propre et les sous-espaces propres sont de dimension
.
Conclusion : Les valeurs propres de
sont les réels
où
.
Le sous-espace propre associé à
est
.
