Eléments propres d'un endomorphisme
Définition :
Un scalaire
est valeur propre d'un endomorphisme
si :
.
Le spectre d'un endomorphisme
est l'ensemble
des valeurs propres de
.
Fondamental :
Propriétés :
Un scalaire
est valeur propre de
si et seulement si
.Si
est valeur propre de
et si
,
est valeur propre de
.Si
est un polynôme annulateur de
, alors :
(racines de
).Si
est polynôme minimal de
, alors :
.
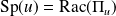Définition :
Un vecteur
est vecteur propre d'un endomorphisme
si
et si :
.
Le sous-espace propre associé à une valeur propre
est :
.
Fondamental :
Propriétés :
Les sous-espaces propres de
sont en somme directe. Les sous-espaces propres de
sont stables par
.
