Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
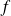et
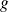deux endomorphismes d'un espace vectoriel
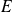de dimension finie qui commutent :
.
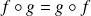On suppose que
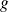est nilpotente.
Question
Montrer que
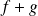est bijective si et seulement si
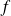est bijective.
Commencez par démontrer que si
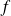n'est pas bijective, alors
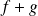n'est pas bijective.
Méthode :
Raisonnement par contraposée
Démontrer que
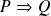équivaut à démontrer que
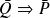(propriétés contraires de
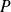et
).
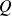Donc on démontre que si
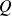est fausse, alors
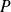est fausse.
On raisonne par contraposée : on suppose que
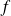n'est pas bijective. Donc
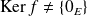. Soit
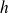la restriction de
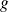à
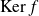. Elle est nilpotente car
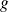l'est. Donc
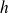n'est pas bijective. Donc :
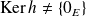. Donc :
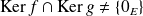.Donc :
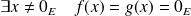, donc :
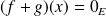, donc :
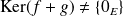.Donc si
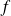n'est pas bijective, alors
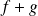n'est pas bijective.Donc par contraposée : si
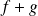est bijective, alors
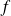est bijective.
Réciproquement, on remarque que :
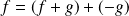et
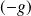est nilpotente.Donc en appliquant ce qui précède, si
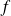est bijective, alors
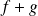est bijective.
Conclusion :
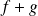est bijective si et seulement si
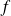est bijective.
Question
Montrer que :
.
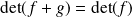Commencez par étudier le cas où
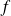n'est pas bijective.
Dans le cas où
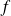est bijective, exprimez
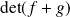comme produit de
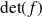par un déterminant égal à
.
Il y a deux cas selon que
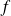est bijective ou pas.
Si
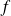n'est pas bijective,
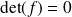, et d'après ce qui précède,
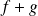n'est pas bijective, donc
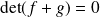.Donc
.
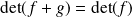Si
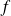est bijective,
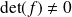et
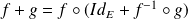.Donc
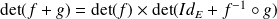.Or
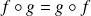, donc :
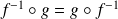, et donc :
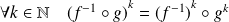.Or
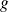est nilpotente, donc il existe un entier
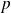tel que
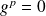, donc
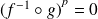.Donc le polynôme
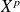est un polynôme annulateur de l'endomorphisme
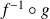.Donc le polynôme caractéristique de
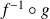divise
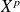. Il est de degré
et de coefficient dominant
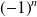. Donc ce polynôme caractéristique est :
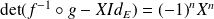.Donc :
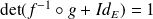. Donc :
.
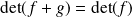Conclusion :
.
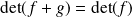