Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
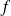 et
et
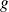 deux endomorphismes d'un espace vectoriel
deux endomorphismes d'un espace vectoriel
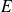 de dimension
de dimension
 tels que
tels que
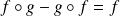 .
.
Question
Montrer que
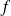 est nilpotente.
est nilpotente.
Exprimez
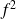 , puis déterminez par récurrence une relation entre les puissances de
, puis déterminez par récurrence une relation entre les puissances de
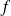 et
et
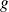 .
.
Ensuite, interprétez la relation obtenue en termes de valeurs propres.
Il s'agit de montrer qu'il existe une puissance de
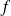 qui est nulle. Donc étudions les différentes puissances de
qui est nulle. Donc étudions les différentes puissances de
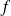 .
.
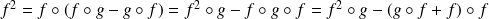 .
.
Donc :
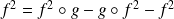 . Donc :
. Donc :
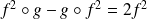 .
.
Montrons par récurrence que, pour tout entier
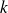 :
:
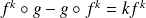 .
.
Initialisation : Elle a déjà été faite.
Hérédité : Soit
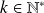 tel que
tel que
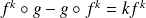 .
.
Donc :
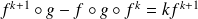 . Donc :
. Donc :
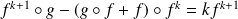 .
.
Donc :
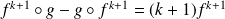 .
.
Conclusion :
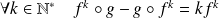 .
.
Soit
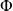 l'application qui à tout
l'application qui à tout
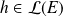 associe l'endomorphisme
associe l'endomorphisme
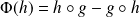 .
.
On vérifie facilement que cette application
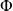 est un endomorphisme de
est un endomorphisme de
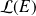 .
.
D'après ce qui précède :
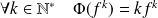 . Donc si
. Donc si
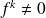 ,
,
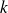 est valeur propre de
est valeur propre de
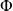 .
.
Or
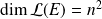 . Donc
. Donc
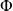 a au plus
a au plus
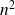 valeurs propres.
valeurs propres.
Donc il existe au plus
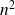 puissances de
puissances de
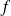 qui sont non nulles. Donc il en existe une qui est nulle.
qui sont non nulles. Donc il en existe une qui est nulle.
Conclusion : L'application
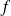 est nilpotente.
est nilpotente.
Question
Si
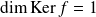 , quelle est la dimension du noyau de
, quelle est la dimension du noyau de
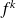 si
si
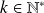 .
.
Etudiez la suite de terme général :
 .
.
Soit
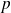 le plus petit entier tel que
le plus petit entier tel que
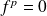 . Donc
. Donc
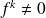 si
si
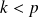 et
et
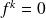 si
si
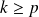 .
.
Donc
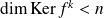 si
si
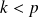 et
et
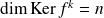 si
si
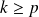 . Soit
. Soit
 .
.
Pour tout entier
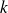 :
:
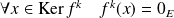 , donc :
, donc :
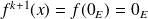 .
.
Donc :
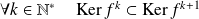 . Donc la suite
. Donc la suite
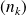 est croissante.
est croissante.
Supposons que :
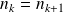 . Donc :
. Donc :
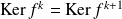 .
.
Soit
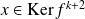 , donc
, donc
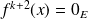 , donc
, donc
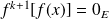 , donc
, donc
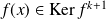 .
.
Donc
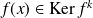 , donc
, donc
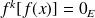 , donc
, donc
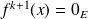 , donc
, donc
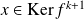 .
.
Donc
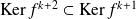 , donc
, donc
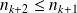 . Or la suite
. Or la suite
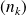 est croissante. Donc
est croissante. Donc
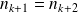 .
.
Donc s'il existe
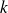 tel que
tel que
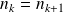 , alors
, alors
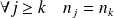 . Donc
. Donc
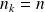 .
.
Donc la suite
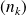 est strictement croissante jusqu'au rang
est strictement croissante jusqu'au rang
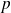 , puis stationnaire.
, puis stationnaire.
De plus, pour tout
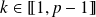 :
:
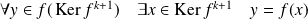 , donc
, donc
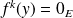 , donc
, donc
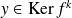 .
.
Donc
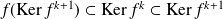 . Donc le sous-espace
. Donc le sous-espace
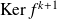 est stable par
est stable par
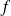 .
.
Donc on peut considérer la restriction
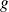 de
de
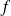 à
à
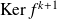 . On a :
. On a :
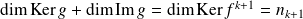 .
.
Or :
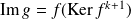 , donc
, donc
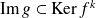 , donc
, donc
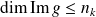 .
.
Et :
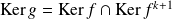 , donc
, donc
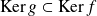 , donc
, donc
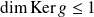 .
.
Donc :
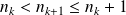 . Or
. Or
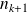 est un entier, donc
est un entier, donc
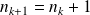 si
si
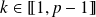 .
.
Donc :
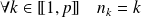 car
car
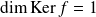 . Or :
. Or :
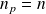 . Donc :
. Donc :
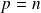 .
.
Conclusion :
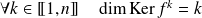 et
et
 .
.





