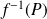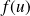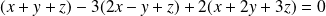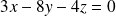Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
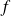l'application de
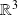dans
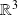définie par :
.
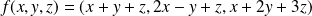Question
Démontrer que l'application
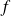est linéaire.
Pour tous vecteurs
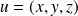et
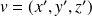, et tout réel
:
.
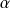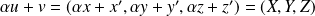Donc :
.
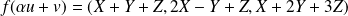Or :
.
Donc :
.
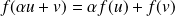Conclusion : L'application
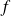est linéaire.
Question
Déterminer l'image par
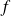du plan vectoriel
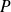d'équation :
.
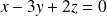Utilisez l'image d'une famille génératrice de
.
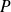Un vecteur
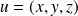appartient à
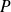si et seulement si :
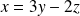, donc si :
.
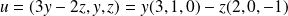Donc les vecteurs
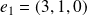et
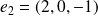forment une famille génératrice du plan
.
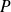Donc
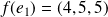et
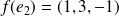forment une famille génératrice de
.
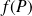Donc un vecteur
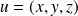appartient à
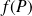si et seulement si il existe des réels
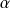et
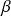tels que
.
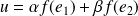Or
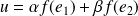équivaut à :
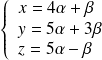, donc à :
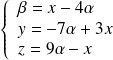, donc à :
.
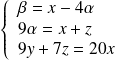Conclusion : L'image directe
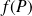est le plan d'équation
.
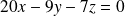