Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
,
,
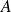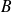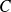et
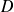quatre matrices de
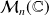telles que
.
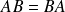Question
Montrer que si
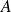est inversible, alors
.
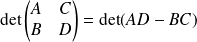Pour calculer le déterminant, multipliez la matrice par une matrice dont le déterminant vaut
.
Pour calculer
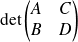, multiplions la matrice
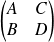par une matrice dont le déterminant vaut
, par exemple par une matrice de la forme :
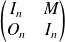où
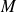est une matrice de
.
.
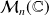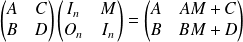Donc :
.
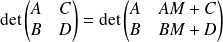Si
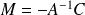, alors
.
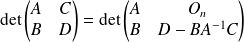Donc :
.
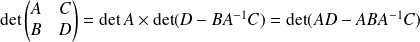Or :
.
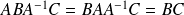Conclusion : Si
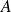est inversible et
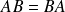, alors
.
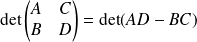Complément :
Ce résultat est encore vrai même si la matrice
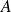n'est pas inversible.
En effet, le polynôme caractéristique de
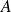n'a qu'un nombre fini de racines. Donc il existe une infinité de réels
tels que
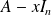soit inversible.
Et, pour tous ces réels
:
.
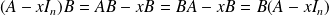Donc, d'après l'étude précédente:
.
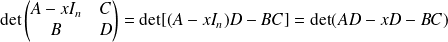Donc le polynôme
possède une infinité de racines. Donc c'est le polynôme nul.
Donc
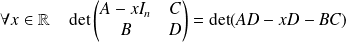, en particulier pour
.
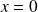Conclusion : Si
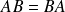, alors
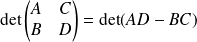, même si
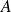n'est pas inversible.
