Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
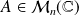et
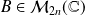la matrice écrite par blocs :
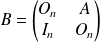où
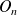désigne la matrice nulle de
.
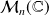Question
Montrer que
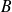est inversible si et seulement si
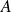est inversible.
Cherchez une matrice
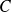écrite par blocs telle que :
.
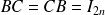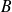est inversible si et seulement si il existe une matrice
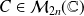telle que
.
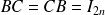Soit
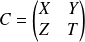où
,
,
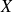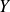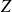et
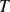sont des matrices de
.
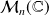Donc
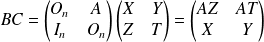et
.
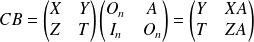Donc
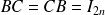si et seulement si :
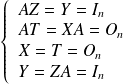, donc si :
.
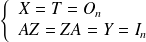Donc
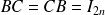si et seulement si
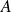est inversible et
.
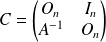Conclusion : La matrice
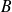est inversible si et seulement si la matrice
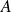est inversible.
Question
Calculer
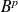pour
.
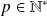Calculez les puissances de
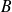pour
,
,
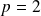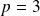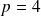et conjecturez une formule que vous démontrerez par récurrence.
Pour
:
.
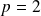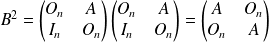Pour
:
.
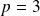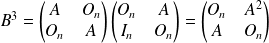Pour
:
.
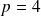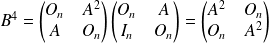On conjecture que :
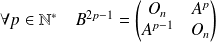et
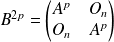. Montrons le par récurrence.
Initialisation : Elle est déjà faite.
Hérédité : Soit
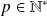tel que
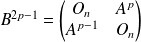et
.
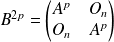Donc :
.
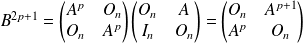Et :
.
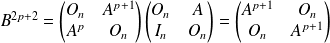Conclusion :
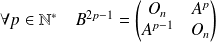et
.
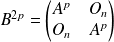