Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Dans
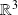, déterminer les coordonnées du vecteur
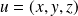dans la base
:
,
,
.
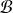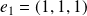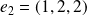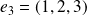Utiliser la matrice de passage de la base canonique à la base
.
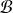La matrice de passage de la base canonique à cette base
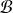est :
.
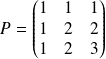Le vecteur
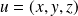a pour matrice
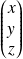dans la base canonique et
dans
.
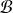Donc :
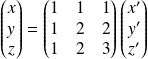, donc :
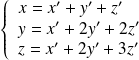, donc :
.
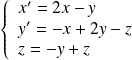Conclusion : Les coordonnées du vecteur
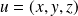dans la base
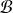sont
.
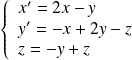On peut en déduire la matrice inverse de
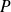qui est la matrice de passage de la base
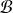à la base canonique :
.
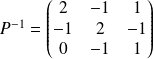Autre méthode : On aurait pu procéder inversement en déterminant d'abord la matrice
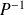, puis les coordonnées de
en utilisant la relation :
.
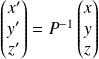On peut obtenir
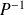soit en inversant
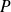, soit en exprimant les vecteurs de la base canonique en fonction des vecteurs de la base
.
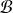