Matrices de vecteurs
Définition :
Matrice d'un vecteur
Si
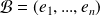 est une base de
est une base de
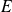 , à tout vecteur
, à tout vecteur
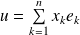 , associe la matrice colonne
, associe la matrice colonne
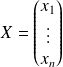 .
.
Inversement, toute matrice colonne peut être interprétée comme la matrice d'un vecteur.
Définition :
Matrice d'une famille de vecteurs
Si
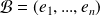 est une base de
est une base de
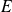 , à toute famille de vecteurs
, à toute famille de vecteurs
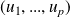 on associe la matrice dont les vecteurs colonnes sont les matrices des vecteurs
on associe la matrice dont les vecteurs colonnes sont les matrices des vecteurs
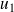 , ...,
, ...,
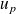 dans la base.
dans la base.
Inversement, toute matrice peut être interprétée comme la matrice d'une famille de vecteurs.
Définition :
Changement de base
Si
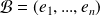 et
et
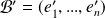 sont deux bases de
sont deux bases de
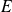 , la matrice de passage de
, la matrice de passage de
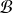 à
à
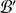 est la matrice
est la matrice
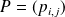 avec
avec
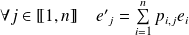 .
.
Fondamental :
Propriétés :
Toute matrice de passage d'une base
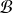 à une base
à une base
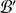 est inversible et son inverse est la matrice de passage de
est inversible et son inverse est la matrice de passage de
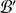 à
à
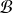 .
.Si un vecteur
 a pour matrice
a pour matrice
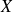 dans
dans
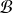 et
et
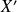 dans
dans
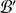 , alors :
, alors :
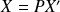 .
.





