Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit une matrice
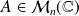telle que :
.
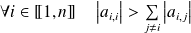Question
Montrer que la matrice
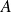est inversible.
Raisonnez par l'absurde.
Montrez que si
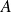n'est pas inversible, il existe une matrice colonne
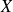telle que
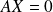, et introduisez le plus grand des
.
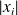On raisonne par l'absurde en supposant
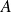non inversible, donc
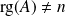, donc ses vecteurs colonnes forment une famille liée.
Donc il existe
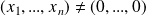tel que :
.
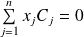Donc il existe
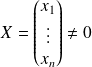tel que
.
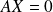Donc :
.
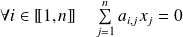Soit
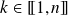tel que
.
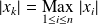Donc
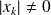car l'un au moins des
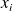est non nul.
Or :
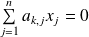, donc
.
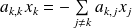Donc :
.
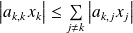Donc :
.
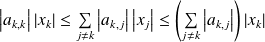Donc :
.
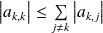Or d'après l'hypothèse :
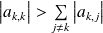. On aboutit donc à une contradiction.
Conclusion : La matrice
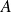est inversible.
