Rang d'une matrice carrée
Définition :
Le rang d'une matrice
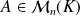est le rang de la famille de ses vecteurs colonnes
.
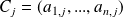Le rang de la matrice est donc la dimension du sous-espace vectoriel de
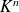engendré par ses vecteurs colonnes.
Fondamental :
Propriétés :
Une matrice
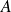est inversible si et seulement si
. 
.
. 
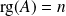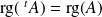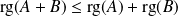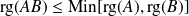.Si
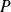est une matrice inversible :
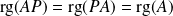.Si
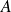et
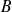sont deux matrices semblables (c'est-à-dire si
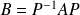), alors :
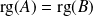.Si
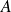est une matrice triangulaire avec
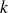zéros sur la diagonale, alors
.
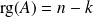Pour déterminer le rang d'une matrice, on peut trianguler la matrice, c'est-à-dire trouver une matrice inversible
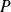et une matrice triangulaire
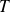telles que
.
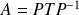S'il y a
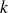zéros sur la diagonale de
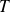, alors
.
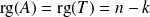