Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Soit un entier
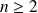 . Déterminer les matrices de
. Déterminer les matrices de
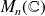 qui commutent avec toutes les matrices symétriques.
qui commutent avec toutes les matrices symétriques.
Utilisez la base canonique
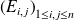 de
de
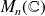 .
.
Commencez par exprimer le produit
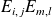 de deux vecteurs de la base.
de deux vecteurs de la base.
Vous en déduirez ensuite les produits
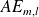 et
et
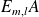 d'une matrice
d'une matrice
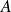 par un des vecteurs de la base.
par un des vecteurs de la base.
Remarquez que les matrices
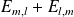 sont symétriques.
sont symétriques.
Préliminaire
Soit
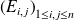 la base canonique de
la base canonique de
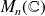 .
.
Soient
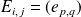 donc
donc
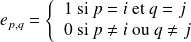 , et
, et
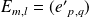 donc
donc
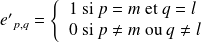 .
.
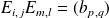 avec
avec
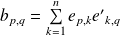 . Donc :
. Donc :
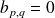 si
si
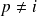 ou
ou
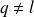 .
.
Et :
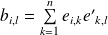 a un seul terme non nul
a un seul terme non nul
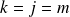 , donc
, donc
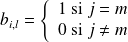 .
.
Donc
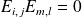 si
si
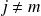 , et
, et
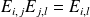 .
.
Donc, si
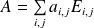 , alors
, alors
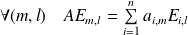 et
et
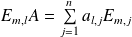 .
.
Solution
Soit
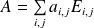 une matrice qui commute avec toutes les matrices symétriques.
une matrice qui commute avec toutes les matrices symétriques.
Donc en particulier :
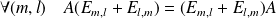 .
.
Donc :
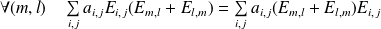 .
.
Donc :
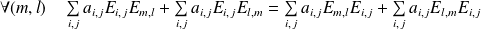 .
.
Donc :
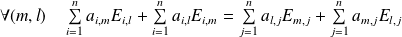 .
.
Donc par unicité des coordonnées dans la base canonique :
si
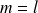 :
:
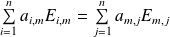 , donc
, donc
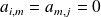 si
si
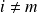 ou
ou
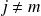 .
.Donc la matrice
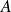 est diagonale
est diagonalesi
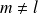 :
:
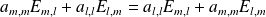 , donc
, donc
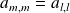 .
.Donc il existe un complexe
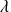 tel que
tel que
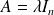 .
.
La réciproque est évidente.
Conclusion : Les matrices qui commutent avec toutes les matrices symétriques sont les matrices de la forme
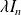 où
où
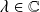 .
.
Question
Déterminer les matrices de
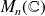 qui commutent avec toutes les matrices antisymétriques.
qui commutent avec toutes les matrices antisymétriques.
Utilisez la base canonique
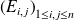 de
de
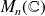 .
.
Remarquez que les matrices
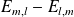 sont antisymétriques.
sont antisymétriques.
Soit
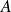 une matrice qui commute avec toutes les matrices antisymétriques, donc en particulier avec toutes les matrices
une matrice qui commute avec toutes les matrices antisymétriques, donc en particulier avec toutes les matrices
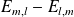 si
si
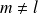 .
.
Donc :
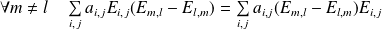 .
.
Donc :
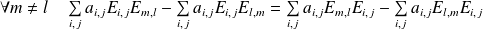 .
.
Donc :
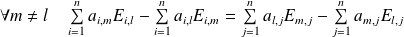 .
.
Donc par unicité des coordonnées dans la base
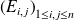 :
:
si
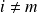 et
et
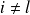 :
:
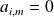 et
et
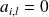 .
.si
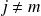 et
et
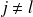 :
:
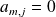 et
et
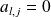 .
.Donc la matrice
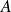 est diagonale.
est diagonale.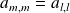 .
.Donc il existe un complexe
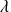 tel que
tel que
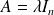 .
.
La réciproque est évidente.
Conclusion : Les matrices qui commutent avec toutes les matrices antisymétriques sont les matrices de la forme
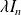 où
où
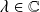 .
.





