Transposition
Définition :
Si
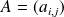 appartient à
appartient à
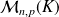 , sa transposée
, sa transposée
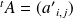 appartient à
appartient à
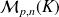 et est définie par :
et est définie par :
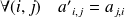 .
.
La matrice transposée est obtenue en intervertissant les lignes et les colonnes.
Exemple :
Si
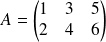 , sa transposée est :
, sa transposée est :
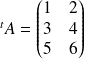 .
.
Fondamental :
Propriétés :
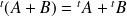 .
. 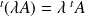 .
. 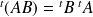 .
.
Définition :
Une matrice carrée
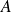 est symétrique si :
est symétrique si :
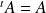 .
.
Une matrice carrée
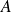 est antisymétrique si :
est antisymétrique si :
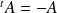 .
.





