Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère un triangle rectangle dont les longueurs
 ,
,
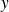 et
et
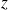 des trois côtés sont des nombres entiers.
des trois côtés sont des nombres entiers.
Les entiers
 ,
,
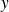 et
et
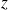 sont donc solutions de l'équation :
sont donc solutions de l'équation :
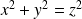 .
.
On suppose d'abord que
 et
et
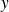 sont premiers entre eux.
sont premiers entre eux.
Question
Démontrer que :
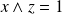 et
et
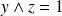 .
.
Raisonnez par l'absurde.
Montrons que
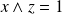 en raisonnant par l'absurde.
en raisonnant par l'absurde.
Supposons que
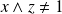 . Donc il admet un diviseur premier
. Donc il admet un diviseur premier
 .
.
Et
 divise
divise
 et
et
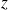 , donc
, donc
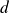 divise
divise
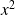 et
et
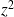 , donc
, donc
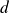 divise
divise
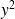 .
.
Or
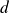 est premier, donc
est premier, donc
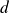 divise
divise
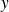 , donc
, donc
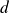 est un diviseur premier de
est un diviseur premier de
 et de
et de
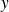 .
.
Or
 et
et
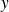 sont premiers entre eux. On aboutit donc à une contradiction.
sont premiers entre eux. On aboutit donc à une contradiction.
Donc :
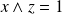 .
.
Les entiers
 et
et
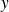 jouent des rôles symétriques. Donc :
jouent des rôles symétriques. Donc :
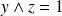 .
.
Conclusion : Si
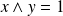 , alors
, alors
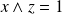 et
et
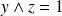 .
.
Question
Démontrer que
 et
et
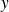 n'ont pas la même parité.
n'ont pas la même parité.
Raisonnez par l'absurde.
Comme
 et
et
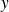 sont premiers entre eux, ils ne peuvent pas être tous les deux pairs.
sont premiers entre eux, ils ne peuvent pas être tous les deux pairs.
Supposons que
 et
et
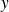 soient tous les deux impairs. Donc
soient tous les deux impairs. Donc
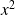 et
et
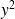 sont impairs.
sont impairs.
Donc
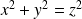 est pair, donc
est pair, donc
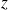 est pair, donc
est pair, donc
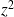 est divisible par
est divisible par
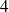 .
.
Or, si
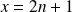 et
et
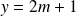 , alors :
, alors :
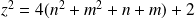 n'est pas divisible par 4.
n'est pas divisible par 4.
On aboutit donc à une contradiction. Donc
 et
et
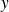 ne sont pas tous les deux impairs.
ne sont pas tous les deux impairs.
Conclusion : Si
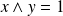 , alors
, alors
 et
et
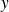 sont de parité différentes.
sont de parité différentes.
On supposera dans la suite que
 est impair et que
est impair et que
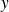 est pair.
est pair.
Question
Démontrer qu'il existe deux entiers
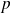 et
et
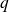 premiers entre eux tels que :
premiers entre eux tels que :
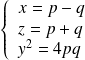 .
.
Factorisez
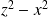 .
.
Comme
 et
et
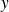 jouent des rôles symétriques, on peut supposer
jouent des rôles symétriques, on peut supposer
 impair et
impair et
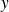 pair.
pair.
Donc
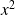 est impair et
est impair et
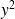 est pair, et donc
est pair, et donc
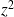 est impair, donc
est impair, donc
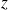 est impair.
est impair.
Donc
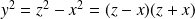 est le produit de deux nombres pairs.
est le produit de deux nombres pairs.
Donc il existe deux entiers
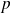 et
et
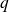 tels que :
tels que :
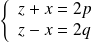 , donc :
, donc :
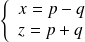 et
et
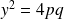 .
.
Le PGCD de
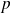 et
et
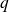 divise
divise
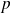 et
et
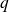 , donc divise
, donc divise
 et
et
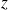 . Or :
. Or :
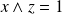 , donc :
, donc :
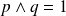 .
.
Conclusion : Si
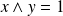 , alors il existe deux entiers
, alors il existe deux entiers
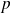 et
et
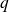 premiers entre eux tels que :
premiers entre eux tels que :
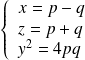 .
.
Question
En déduire qu'il existe deux entiers
 et
et
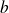 premiers entre eux tels que :
premiers entre eux tels que :
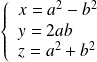 .
.
Démontrez que
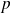 et
et
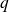 sont des carrés en utilisant leur décomposition en facteurs premiers.
sont des carrés en utilisant leur décomposition en facteurs premiers.
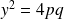 , donc
, donc
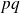 est un carré :
est un carré :
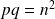 .
.
Soit
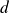 un diviseur premier de
un diviseur premier de
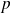 . Donc
. Donc
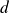 divise
divise
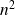 , donc
, donc
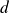 divise
divise
 , donc
, donc
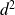 divise
divise
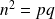 .
.
Or
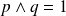 , donc
, donc
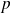 et
et
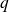 n'ont pas de diviseur premier commun.
n'ont pas de diviseur premier commun.
Donc
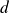 ne divise pas
ne divise pas
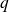 , donc
, donc
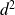 est premier avec
est premier avec
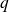 , donc
, donc
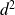 divise
divise
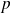 .
.
Donc, dans la décomposition en facteurs premiers de
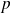 , tous les facteurs ont une puissance paire.
, tous les facteurs ont une puissance paire.
Donc
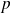 est un carré. Donc il existe un entier
est un carré. Donc il existe un entier
 tel que :
tel que :
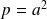 .
.
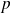 et
et
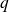 jouent des rôles symétriques, donc il existe un entier
jouent des rôles symétriques, donc il existe un entier
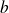 tel que
tel que
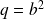 .
.
Le PGCD de
 et
et
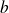 divise
divise
 et
et
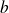 , donc il divise
, donc il divise
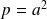 et
et
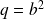 . Or :
. Or :
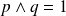 .
.
Donc :
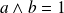 . Donc
. Donc
 et
et
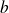 sont premiers entre eux.
sont premiers entre eux.
Conclusion : Si
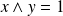 , alors il existe deux entiers
, alors il existe deux entiers
 et
et
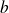 premiers entre eux tels que :
premiers entre eux tels que :
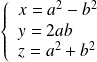 .
.
Question
En déduire, dans le cas général, tous les triplets
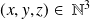 tels que
tels que
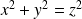 .
.
Ramenez-vous au cas où
 et
et
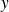 sont premiers entre eux.
sont premiers entre eux.
Soit
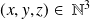 tels que :
tels que :
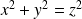 et soit
et soit
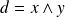 .
.
Donc il existe des entiers
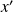 et
et
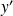 tels que
tels que
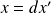 ,
,
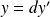 et
et
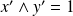 .
.
Donc
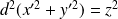 . Donc
. Donc
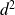 divise
divise
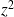 , donc
, donc
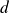 divise
divise
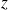 , donc il existe un entier
, donc il existe un entier
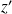 tel que :
tel que :
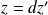 .
.
Donc l'équation
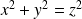 équivaut à
équivaut à
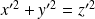 avec
avec
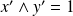 .
.
On retrouve donc le problème déjà étudié.
Conclusion : Les triplets solutions sont de la forme
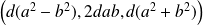 où
où
 ,
,
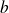 et
et
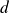 sont des entiers naturels avec
sont des entiers naturels avec
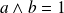 .
.





