Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Déterminer, suivant les valeurs de l'entier
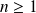 , le PGCD de
, le PGCD de
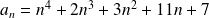 et
et
 .
.
Démontrez que si
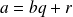 , alors
, alors
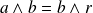 même si
même si
 n'est pas le reste de la division de
n'est pas le reste de la division de
 par
par
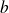 .
.
Appliquez ce résultat à
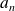 et
et
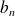 .
.
Remarque :
Si
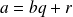 , alors
, alors
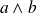 divise
divise
 et
et
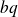 , donc divise
, donc divise
 . Donc
. Donc
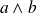 divise
divise
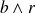 .
.
Inversement,
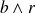 divise
divise
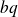 et
et
 , donc divise
, donc divise
 . Donc
. Donc
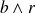 divise
divise
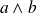 .
.
Donc si
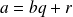 , alors :
, alors :
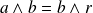 .
.
La propriété est vraie même si
 n'est pas le reste de la division de
n'est pas le reste de la division de
 par
par
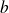 .
.
Soit
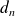 le PGCD de
le PGCD de
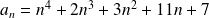 et
et
 .
.
Or :
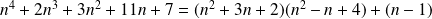 .
.
Donc :
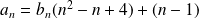 . Donc :
. Donc :
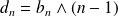 .
.
Or :
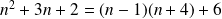 . Donc :
. Donc :
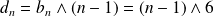 .
.
Effectuons la division de
 par
par
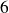 :
:
 avec
avec
 .
.
Si
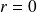 , alors
, alors
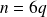 et
et
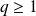 , donc
, donc
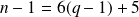 , donc
, donc
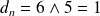 .
.
Si
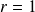 , alors
, alors
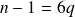 , donc
, donc
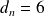 .
.
Si
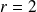 , alors
, alors
 , donc
, donc
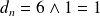 .
.
Si
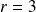 , alors
, alors
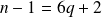 , donc
, donc
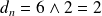 .
.
Si
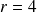 , alors
, alors
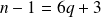 , donc
, donc
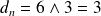 .
.
Si
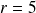 , alors
, alors
 , donc
, donc
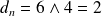 .
.
Conclusion :
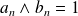 s'il existe un entier
s'il existe un entier
 tel que
tel que
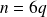 ou
ou
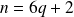 .
.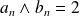 s'il existe un entier
s'il existe un entier
 tel que
tel que
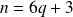 ou
ou
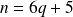 .
.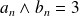 s'il existe un entier
s'il existe un entier
 tel que
tel que
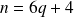 .
.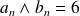 s'il existe un entier
s'il existe un entier
 tel que
tel que
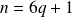 .
.





