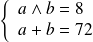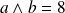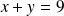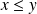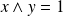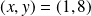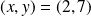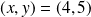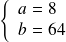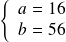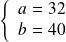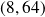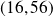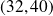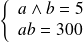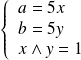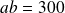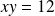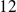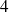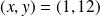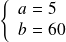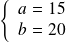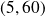Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
et
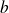deux entiers naturels non nuls tels que
.
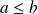Question
Question
Question
Déterminer tous les couples
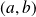tels que :
.
Toujours la même méthode !
Soit
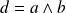. Donc il existe
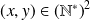tel que :
.
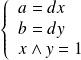De plus
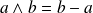, donc
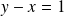, donc
.
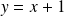Tout entier
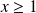est premier avec
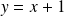car leur PGCD divise
.
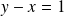Et :
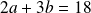, donc :
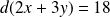. Donc
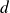est un diviseur de
.
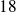Les diviseurs de
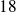sont :
,
,
,
,
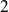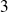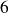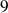et
.
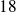Or
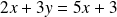, donc :
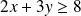. Donc
.
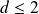Si
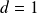, on obtient :
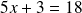, donc
.
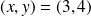Si
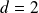, on obtient :
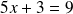qui n'a pas de solution entière.
On obtient donc
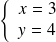, donc
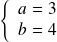qui vérifie bien
.
Conclusion : Il y a un unique couple solution
.
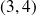