Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer que, pour tout entier naturel
, il existe un unique polynôme
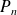tel que :
.
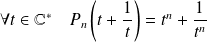Préciser son degré et son coefficient dominant.
Commencez par démontrer l'unicité du polynôme, puis démontrez son existence par récurrence double.
La fonction
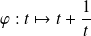est définie, impaire et de classe
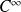sur
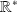et
.
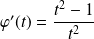Donc
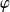est continue et strictement décroissante sur
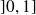, puis strictement croissante sur
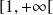. Et :
.
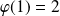De plus
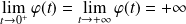. Donc
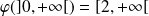et
.
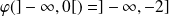On peut déjà remarquer qu'il y a unicité car si deux polynômes convenaient, ils coïncideraient pour tout
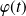, donc au moins sur
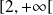, donc ils seraient égaux.
Il reste donc à démontrer l'existence des polynômes. Examinons le cas des premières valeurs de
.
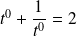, donc
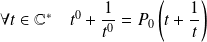en posant
.
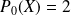De même :
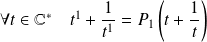en posant
.
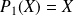Et :
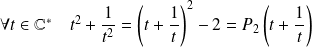en posant
.
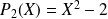Donc
,
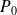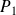et
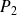existent. On a :
,
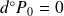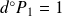et
.
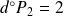Mais, le coefficient dominant de
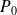est
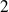, alors que ceux de
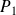et de
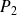sont
.
On conjecture que
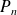existe, que son degré est
et que son coefficient dominant est
si
.
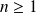Soit
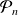cet ensemble de propriétés. On raisonne par récurrence double pour montrer que
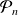est vraie pour tout entier
.
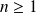Initialisation : Elle est déjà faite car
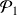et
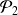sont vraies.
Hérédité : Soit
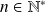tel que
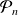et
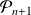soient vraies.
Donc :
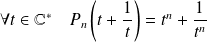et
.
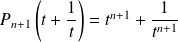Or :
.
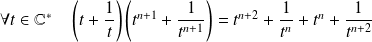Donc :
.
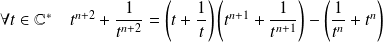Donc :
.
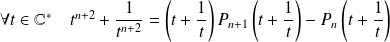Donc
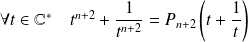en posant :
.
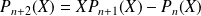Donc
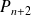existe et
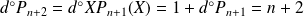car
.
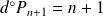Le coefficient dominant de
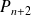est celui de
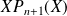, donc celui de
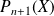, donc ce coefficient est égal à
.
Conclusion : La propriété
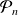est vraie pour tout
.
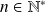De plus
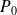existe et
.
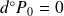Conclusion : Pour tout entier
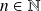, il existe un unique polynôme
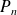tel que :
.
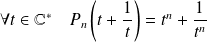Son degré est
et son coefficient dominant est
si
.
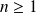Question
Déterminer les racines du polynôme
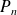. En déduire sa factorisation.
Cherchez pour quelles valeurs de
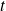le complexe
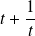est une racine de
.
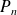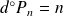, donc
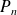a au plus
racines distinctes. Or :
.
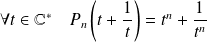Donc si
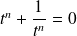, alors
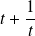est une racine de
.
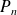Or
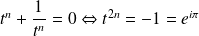. Donc
.
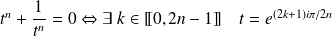Donc si
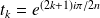, une racine de
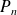est :
.
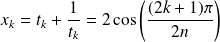Or :
.
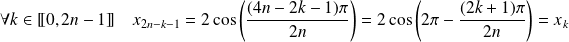Donc :
,
, ...,
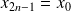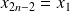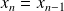. Il reste
racines
,
, ...,
.
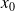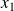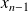Et :
.
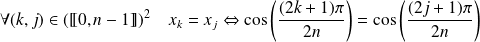Or :
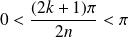et
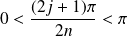. Donc :
.
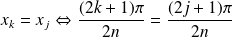Donc :
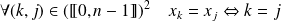. Donc
,
, ...,
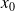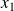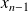sont distincts.
Conclusion :
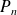admet
racines réelles distinctes :
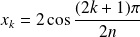pour
.
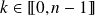Donc sa factorisation est :
.
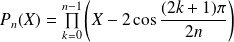Question
Montrer que, pour tout
:
.
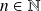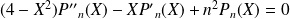Démontrez que :
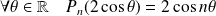, puis dérivez.
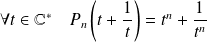. Donc :
.
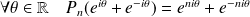Donc :
.
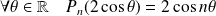Donc en dérivant successivement deux fois :
.
.
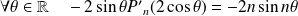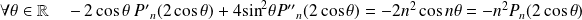Or :
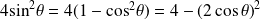
On pose :
.
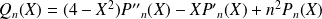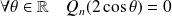. Donc le polynôme
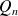admet une infinité de racines. Donc
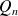est le polynôme nul.
Conclusion :
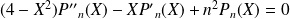pour tout
.
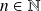Remarque :
Cette relation peut permettre de calculer les coefficients du polynôme
.
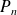Si
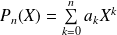, alors
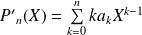et
.
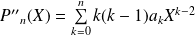Donc :
.
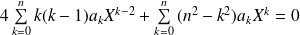Donc :
.
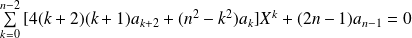Donc :
,
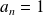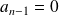et :
.
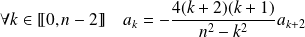Donc :
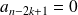et
.
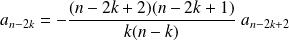Donc :
.
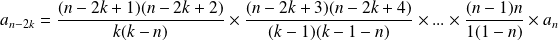Donc :
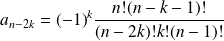si
.
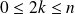Donc :
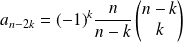si
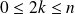et
.
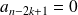Conclusion :
Dans le cas où
est pair (
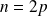), on a :
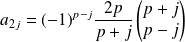et
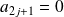.Donc le polynôme est pair et :
.
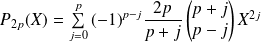Dans le cas où
est impair (
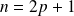), on a :
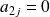et
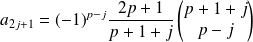.Donc le polynôme est impair et :
.
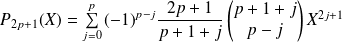