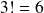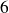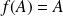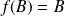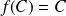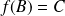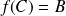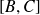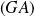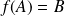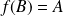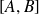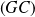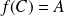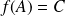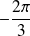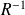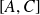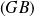Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
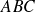un triangle équilatéral direct du plan affine euclidien orienté et
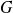son centre de gravité.
Question
Démontrer que l'ensemble
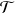des isométries du plan qui conservent globalement le triangle
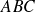est un groupe pour la composition des applications.
Démontrez que
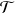est un sous-groupe des isométries du plan.
L'ensemble
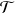est inclus dans l'ensemble des isométries du plan et non vide car l'identité du plan appartient à
.
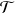Si
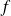et
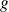sont deux éléments de
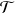, ce sont des isométries qui conservent le triangle, donc leur composée est une isométrie et
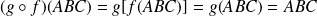. Donc :
.
Si
,
est une isométrie (donc bijective) qui conserve le triangle, donc
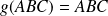. Sa réciproque est une isométrie et
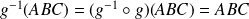. Donc
.
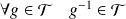Donc
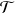est un sous-groupe du groupe des isométries du plan.
Conclusion : L'ensemble
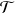des isométries du plan affine euclidien orienté qui conservent globalement le triangle
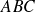est un groupe pour la composition des applications.
Question
Déterminer l'ensemble
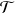des isométries du plan qui conservent globalement le triangle
.
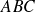Commencez par démontrer que
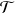est égal à l'ensemble des isométries du plan qui conservent globalement
.
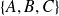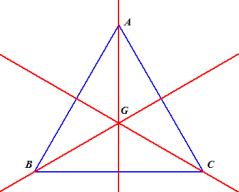
Le triangle
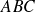est la réunion de trois segments de longueur
.
Une isométrie transforme un segment en un segment de même longueur. Donc il est évident que si une isométrie conserve globalement les sommets du triangle, alors elle conserve globalement le triangle.
Réciproquement, si
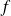appartient à
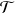, le segment
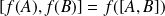est inclus dans l'un des côtés du triangle et de longueur
. Donc le segment
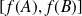est l'un des côtés du triangle. Donc
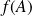et
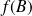sont des sommets du triangle. Le raisonnement est le même pour
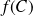. Donc
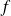conserve globalement les sommets du triangle.
Donc
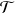est l'ensemble des isométries telles que
.
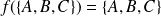Comme
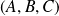est un repère affine du plan, les images
,
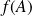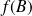et
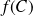déterminent de manière unique l'isométrie
.
Il y a
|  |
Conclusion :
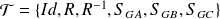où
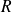est la rotation de centre
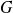et d'angle
.
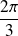