Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Pour tout
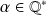 tel que
tel que
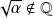 , on définit l'ensemble :
, on définit l'ensemble :
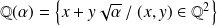 .
.
Question
Montrer que l'ensemble
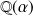 muni de l'addition et de la multiplication est un corps.
muni de l'addition et de la multiplication est un corps.
Montrez que
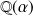 est un sous-corps de
est un sous-corps de
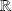 .
.
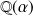 est une partie non vide de
est une partie non vide de
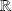 .
.
Soient
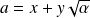 et
et
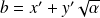 deux éléments de
deux éléments de
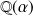 .
.
Donc :
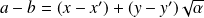 et
et
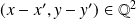 . Donc :
. Donc :
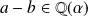 .
.
Comme
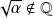 , on a :
, on a :
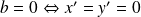 .
.
Donc si
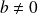 , alors
, alors
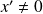 ou
ou
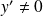 . Et
. Et
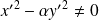 car
car
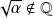 .
.
Donc si
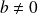 :
:
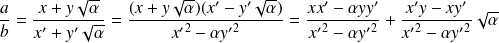 .
.
Or
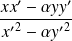 et
et
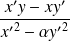 appartiennent à
appartiennent à
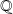 . Donc
. Donc
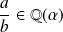 .
.
Donc
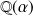 est un sous-corps de
est un sous-corps de
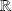 .
.
Conclusion :
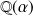 est un corps.
est un corps.
Question
Existe-t-il un isomorphisme de corps entre
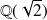 et
et
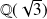 ?
?
Calculez
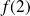 si
si
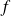 est un isomorphisme et le comparer à
est un isomorphisme et le comparer à
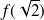 .
.
Supposons qu'il existe un isomorphisme
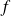 entre
entre
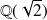 et
et
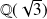 .
.
Donc :
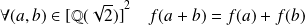 et
et
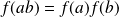 .
.
Et
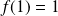 . Donc :
. Donc :
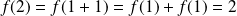 . Or :
. Or :
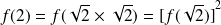 .
.
Or
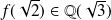 . Donc il existe
. Donc il existe
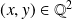 tel que
tel que
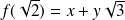 .
.
Donc :
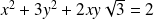 . Donc :
. Donc :
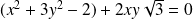 .
.
Or
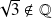 . Donc :
. Donc :
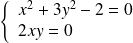 . Donc :
. Donc :
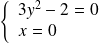 ou
ou
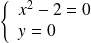 .
.
Or
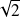 et
et
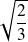 ne sont pas rationnels. Donc ces systèmes n'ont pas de solution.
ne sont pas rationnels. Donc ces systèmes n'ont pas de solution.
Conclusion : Il n'existe pas d'isomorphisme de corps entre
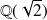 et
et
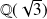 .
.
Question
A quelle condition existe-t-il un isomorphisme de corps entre
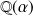 et
et
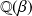 ?
?
Démontrer que
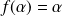 si
si
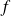 est un isomorphisme et en déduire
est un isomorphisme et en déduire
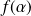 .
.
Supposons qu'il existe un isomorphisme
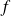 entre
entre
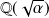 et
et
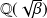 .
.
Donc :
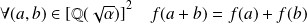 et
et
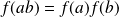 .
.
On a :
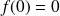 ,
,
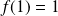 ,
,
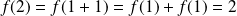 , et par récurrence :
, et par récurrence :
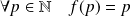 .
.
Donc :
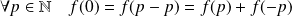 , donc :
, donc :
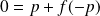 , donc :
, donc :
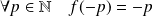 .
.
Or
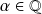 . Donc il existe
. Donc il existe
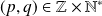 tel que :
tel que :
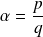 .
.
Donc :
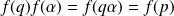 , donc :
, donc :
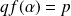 . Donc :
. Donc :
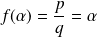 .
.
Ensuite, le raisonnement est le même que dans la question précédente.
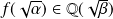 . Donc il existe
. Donc il existe
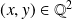 tel que :
tel que :
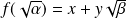 .
.
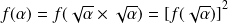 . Donc :
. Donc :
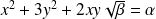 .
.
Or
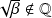 . Donc :
. Donc :
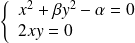 . Donc :
. Donc :
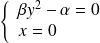 ou
ou
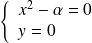 .
.
Or
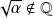 . Donc le système n'a de solution que si
. Donc le système n'a de solution que si
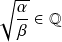 .
.
Réciproquement, si
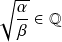 , il existe un rationnel
, il existe un rationnel
 tel que
tel que
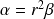 .
.
Donc :
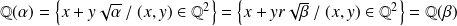 .
.
Donc il y a évidemment un isomorphisme entre
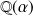 et
et
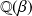 : l'identité.
: l'identité.
Conclusion : Il existe un isomorphisme de corps entre
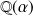 et
et
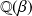 si et seulement si
si et seulement si
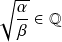 , donc si
, donc si
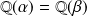 .
.





