Exo 10
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
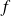 une application d'un ensemble
une application d'un ensemble
 dans un ensemble
dans un ensemble
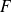 .
.
Question
Soit
 une partie de
une partie de
 . Démontrer que l'on n'a pas toujours
. Démontrer que l'on n'a pas toujours
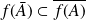 .
.
Trouvez un contre-exemple.
Vous pouvez utiliser l'application
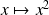 , par exemple.
, par exemple.
Soit
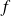 l'application de
l'application de
 dans
dans
 définie par
définie par
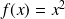 et
et
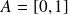 .
.
La fonction
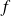 est continue sur
est continue sur
 . La fonction
. La fonction
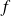 est strictement décroissante sur
est strictement décroissante sur
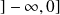 et strictement croissante sur
et strictement croissante sur
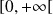 .
.
Donc :
 , et
, et
 .
.
Et :
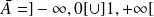 , donc
, donc
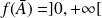 .
.
Conclusion :
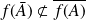 .
.
Question
Démontrer que
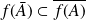 pour toute partie
pour toute partie
 de
de
 si et seulement si
si et seulement si
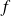 est injective.
est injective.
Démontrez successivement les deux implications.
Remarquez que, parmi les parties de
 , il y a tous les singletons
, il y a tous les singletons
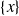 .
.
Montrons successivement les deux implications :
On suppose que :
 . Donc :
. Donc :
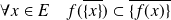 .
.Donc :
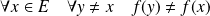 . Donc
. Donc
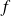 est injective.
est injective.
On suppose que
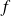 est injective. Soit
est injective. Soit
 une partie de
une partie de
 .
. . Et :
. Et :
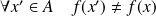 car
car
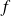 est injective.
est injective.Donc :
 , donc
, donc
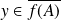 . Donc :
. Donc :
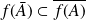 .
.
Conclusion :
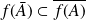 pour toute partie
pour toute partie
 de
de
 si et seulement si
si et seulement si
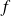 est injective.
est injective.
Question
Question
Démontrer que
 pour toute partie
pour toute partie
 de
de
 si et seulement si
si et seulement si
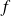 est surjective.
est surjective.
Démontrez successivement les deux implications.
Montrons successivement les deux implications :
On suppose que :
 . Soit
. Soit
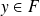 .
.Donc :
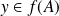 ou
ou
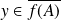 , mais, dans ce cas,
, mais, dans ce cas,
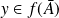 .
.Donc :
 . Donc
. Donc
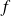 est surjective.
est surjective.
On suppose que
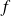 est surjective. Soit
est surjective. Soit
 une partie de
une partie de
 .
. car
car
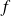 est surjective.
est surjective.Cet élément
 ne peut pas appartenir à
ne peut pas appartenir à
 , car
, car
 .
.Donc :
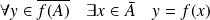 , donc
, donc
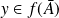 . Donc :
. Donc :
 .
.
Conclusion :
 pour toute partie
pour toute partie
 de
de
 si et seulement si
si et seulement si
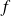 est surjective.
est surjective.
Donc
 pour toute partie
pour toute partie
 de
de
 si et seulement si
si et seulement si
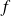 est bijective.
est bijective.