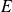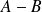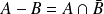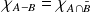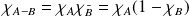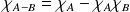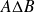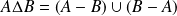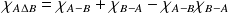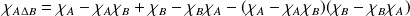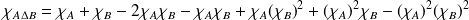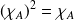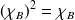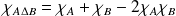Ensembles

Exo 8

Commencez par chercher à résoudre l'exercice par vous-même.

Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.

Une solution détaillée vous est ensuite proposée.

Question

Si et sont deux parties d'un ensemble , déterminer la fonction caractéristique de .

Indice

Utilisez la définition de et les propriétés des fonctions caractéristiques.

Solution

. Donc .

Donc :

Conclusion : .

Question

En déduire la fonction caractéristique de .

Indice

Utilisez la définition de et la question précédente.

Solution

. Donc : .

Donc : .

Donc : .

Or : et .

Conclusion : .

Question

En déduire que : .

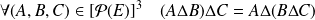Indice

Montrez que .

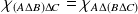Solution

.

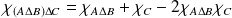Donc : .

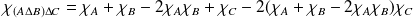Donc : .

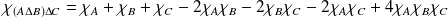La loi est commutative. Donc : .

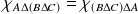Donc : .

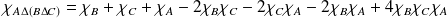Donc : .

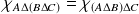Conclusion : .

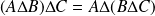La loi 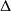est associative.

RemarqueRemarque

On pouvait remarquer que l'expression trouvée pour 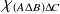est invariante par permutation circulaire sur 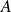, 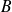et 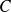, ce qui prouvait l'égalité demandée.

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer Paternité - Pas d'Utilisation Commerciale - Partage des Conditions Initiales à l'IdentiqueRéalisé avec Scenari (nouvelle fenêtre)