Fonction caractéristique d'une partie
Définition :
La fonction caractéristique (ou indicatrice) d'une partie
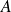d'un ensemble
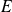est l'application de
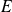dans
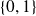, notée
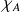, définie par :
.
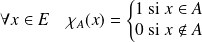Fondamental :
Propriétés :
.
.
.
.
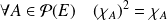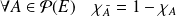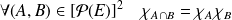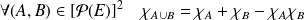Méthode :
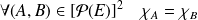si et seulement si
.
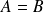Donc démontrer une égalité de deux ensembles équivaut à démontrer l'égalité de leurs fonctions caractéristiques.
Exemple :
On peut utiliser les fonctions caractéristiques :
pour démontrer les lois de Morgan :
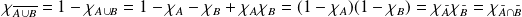.Donc :
.
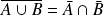ou pour démontrer la distributivité :
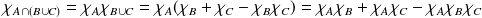. Or
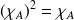.Donc :
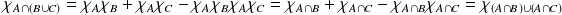.Donc :
.
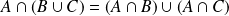