Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
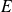et
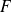deux ensembles.
Question
A quelle condition a-t-on
?
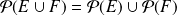Etudiez successivement les deux inclusions.
Etudions successivement les deux inclusions :
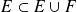, donc toute partie de
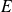est incluse dans
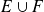, donc
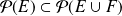.De même
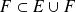, donc
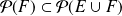.Donc pour tous les ensembles
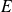et
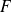, on a
.
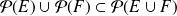On a l'égalité si et seulement si toute partie de
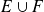est incluse dans
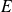ou dans
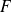.En particulier, il faut que
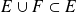ou
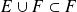, donc que
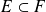ou
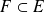.Réciproquement, si
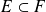, alors
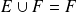, donc
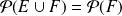. De même si
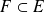, alors
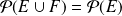.Donc, dans les deux cas, on a :
.
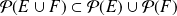Conclusion : Pour tous les ensembles
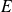et
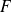, on a
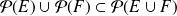, mais il y a égalité si et seulement si
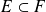ou
.
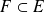