Enoncé
1) Une partie du jeu de « passe dix » consiste à lancer trois dés et à faire la somme des numéros obtenus. On gagne si cette somme est
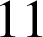ou
.
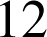Résultat
Correction
Explications
A. Une partie est assimilable à trois tirages successifs avec remise de
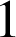numéro parmi
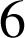. Il y a
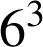parties possibles. Pour obtenir
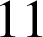, il faut obtenir les nombres,
,
,
,
,
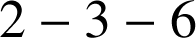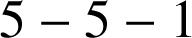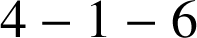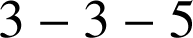et
. Les nombres
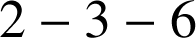peuvent être obtenus de 
soit
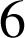façons différentes avec les trois dès, les nombres
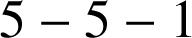de seulement
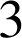façons différentes (il suffit de choisir la place du
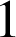). On a donc
parties donnant la somme
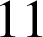, d'où 
.
C. La probabilité de gagner une partie est 
, donc celle de perdre
.
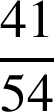On joue
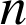parties. Les parties sont indépendantes.
On est donc en présence d'une répétition d'expériences indépendantes. La probabilité cherchée est celle de l'événement contraire à l'événement : « perdre les
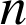parties ».
La probabilité cherchée est donc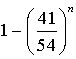 
. Cette probabilité doit être supérieure à
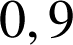, d'où l'on résout : 
.
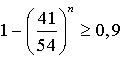On obtient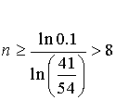 
.