Enoncé
9) Un code à l'entrée d'un immeuble est formé de quatre chiffres distincts pris parmi les chiffres de
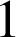à
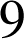. On tape au hasard un code. La probabilité d'avoir tapé un code comportant le chiffre
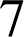et exactement un autre chiffre impair est :
Résultat
Correction
Explications
A. 
. C'est le nombre total de dispositions de quatre chiffres distincts. Il y a équiprobabilité. Le chiffre
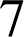est choisi, une possibilité, il reste 
choix possibles pour l'autre chiffre impair et 
choix des deux chiffres pairs distincts. Une fois les chiffres choisis, il reste à les placer, d'où le
!
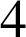C. Le
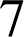est choisi, il faut choisir sa place (
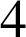), on choisit le deuxième chiffre impair (
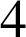) et on le place (
), il reste à choisir et placer les deux chiffres pairs (
).