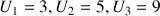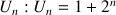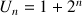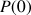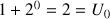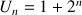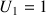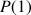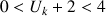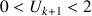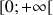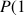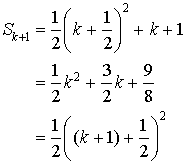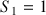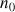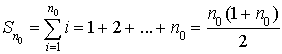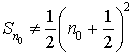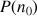Le raisonnement par récurrence
Soit
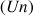la suite définie par : 
.
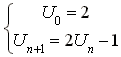Après avoir calculé les premiers termes de la suite, émettre une conjecture sur l'écriture de
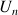en fonction de
puis vérifier cette conjecture à l'aide d'un raisonnement par récurrence.
Soit
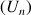la suite définie par : 
.
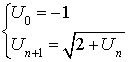Justifier à l'aide d'un raisonnement par récurrence que pour tout entier naturel
non nul,
.
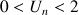Soi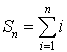t 
et
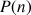la propriété 
.
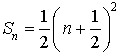Démontrer que pou
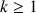r 
, si
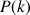est vérifiée alors
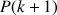est vérifiée. Peut-on en déduire que
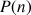est vérifiée pour tout
?
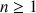