Raisonnement par récurrence
Définition :
Un raisonnement par récurrence permet de démontrer qu'une propriété
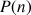qui dépend de l'entier naturel
est vraie pour tout entier naturel
supérieur ou égal à un entier naturel
.
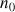On démontre successivement que :
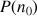est vérifiée,
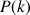si est vérifiée (
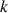entier quelconque supérieur ou égal à
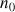) alors
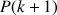est vérifiée (principe d'hérédité de la propriété
).
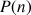On peut alors conclure que
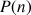est vérifiée pour tout
.
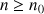L'hypothèse «
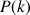est vérifiée » est appelée l'hypothèse de récurrence.
Exemple : Observer : le principe de récurrence
L'animation proposée donne un exemple visuel du caractère héréditaire, ou non, d'une propriété.
Macromedia Flash - 22Ko
