Enoncé
2) Soit
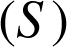 le système :
le système : 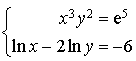 où
où
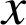 et
et
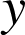 sont des réels.
sont des réels.
Résultat
Correction
Explications
Les propositions A et D sont vraies, les autres sont fausses.
![]() et
et ![]() n'étant définis que pour
n'étant définis que pour
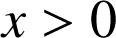 et
et
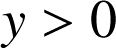 , alors, pour
, alors, pour
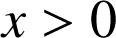 et
et
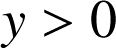 :
:
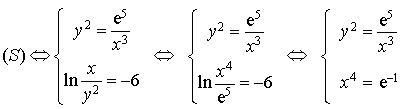
La fonction ![]() est une bijection de
est une bijection de
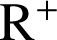 dans
dans
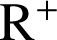 et admet pour réciproque la fonction racine
et admet pour réciproque la fonction racine ![]() :
:
![]() ,
, 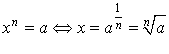 d'où
d'où 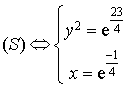
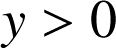 , donc le couple
, donc le couple 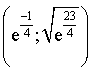 qui peut aussi s'écrire
qui peut aussi s'écrire 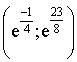 est l'unique solution de
est l'unique solution de
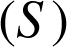 .
.