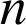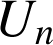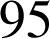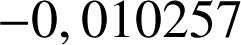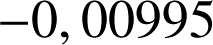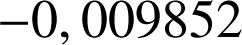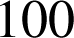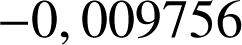Enoncé
4) Soit
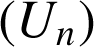 la suite définie pour tout
la suite définie pour tout
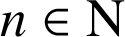 , par
, par 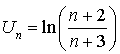 .
.
Résultat
Correction
Explications
A. Pour tout
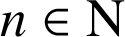 ,
,
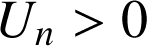
Pour tout
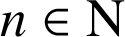 ,
,
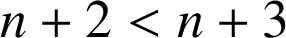 donc
donc ![]() et
et ![]() soit
soit
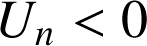 .
.
B. La suite
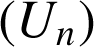 est décroissante
est décroissante
Pour tout
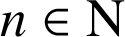 ,
,
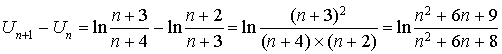
Pour tout
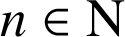 ,
, ![]() d'où
d'où ![]() et
et 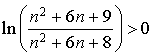 ; la suite
; la suite
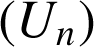 est donc croissante.
est donc croissante.
REMARQUES : l'étude des variations de la fonction
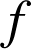 définie par
définie par ![]() sur
sur
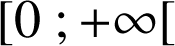 montre que
montre que
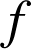 est croissante sur
est croissante sur
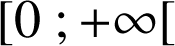 (
(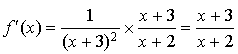 donc
donc
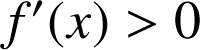 sur
sur
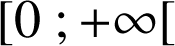 ) et donc que la suite
) et donc que la suite
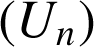 est croissante.
est croissante.
C. 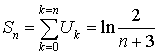
![]()
![]()
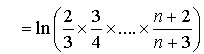
![]()
D. Pour tout ![]() ,
, ![]()
![]() (pour tout
(pour tout
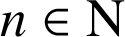 ,
,
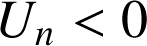 )
)
![]()
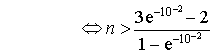
Soit ![]() .
.
Observation de la suite à l'aide d'une machine à calculer ou tableur :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
REMARQUES : la suite
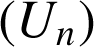 est croissante et majorée par
est croissante et majorée par
 ; elle est donc convergente ;
; elle est donc convergente ; ![]() et
et ![]() , sa limite est zéro.
, sa limite est zéro.