Enoncé
1) La fonction
 est définie sur
est définie sur
 par
par 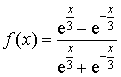 .
.
Résultat
Correction
Explications
A. Pour tout
 ,
,
 existe et
existe et
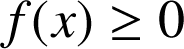
Pour tout
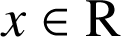 , le dénominateur
, le dénominateur 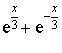 est strictement positif mais le numérateur est positif sur
est strictement positif mais le numérateur est positif sur
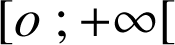 et négatif sur
et négatif sur
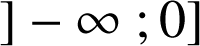 (la fonction exponentielle étant croissante sur
(la fonction exponentielle étant croissante sur
 ,
, 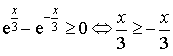 soit
soit
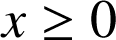 ).
).
B.

![]() et
et ![]() .
.
C. La droite d'équation
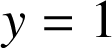 est asymptote à la courbe représentative de
est asymptote à la courbe représentative de

![]()
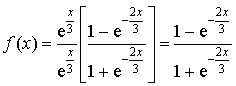 et
et 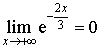
D. La représentation graphique de
 dans un repère orthonormal
dans un repère orthonormal ![]() admet le point
admet le point
 pour centre de symétrie
pour centre de symétrie
La fonction
 est définie sur
est définie sur
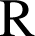 et pour tout
et pour tout
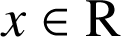 ,
,
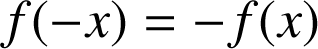 la fonction
la fonction
 est donc impaire.
est donc impaire.
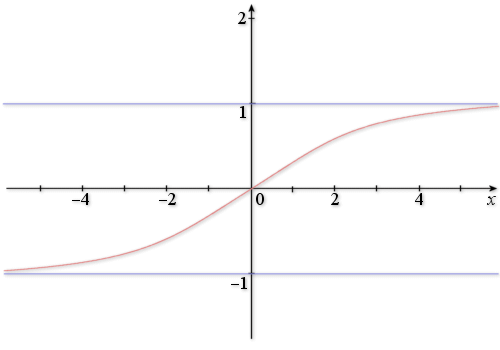
Représentation graphique de f