Enoncé
5) La suite
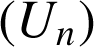 est définie pour tout
est définie pour tout ![]() par
par ![]() .
.
Résultat
Correction
Explications
![]()
En réduisant au même dénominateur :
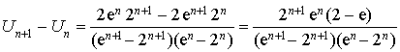
Pour tout ![]() ,
, ![]() et
et ![]() .
.
Pour tout ![]() , la fonction
, la fonction ![]() est croissante sur
est croissante sur
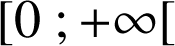 d'où, comme
d'où, comme ![]() ,
, ![]() et
et ![]() ; on en déduit donc que pour tout
; on en déduit donc que pour tout ![]() ,
, ![]() .
.
Pour tout ![]() ,
, ![]() est du signe de
est du signe de ![]() donc négatif. La suite
donc négatif. La suite
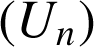 est décroissante.
est décroissante.
Remarque : la proposition A est fausse car pour tout ![]() ,
, ![]() et donc
et donc ![]() .
.