Définition
Propriété, définition :
Soit
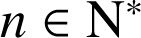et
.
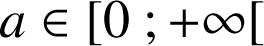L'équation
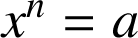admet, dans
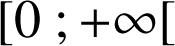, une seule solution qui est notée 
.
et pour
, 
.
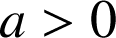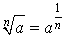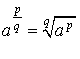où
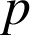et
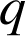sont deux entiers naturels non nuls.
Variations. Courbes :
est dérivable sur
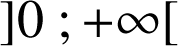; sa dérivée est 
.
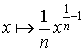est strictement croissante sur
.
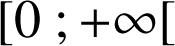est la fonction réciproque de 
sur
.
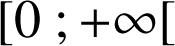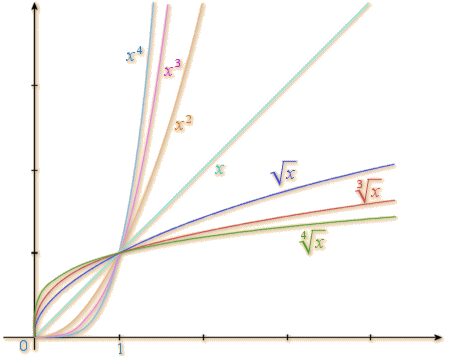
Courbes représentatives de la fonctions racine Nième
