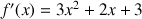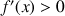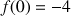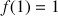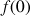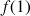Lf est dérivable sur R et sa dérivée est définie par
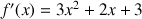 .
.
Pour tout réel
 , on a
, on a
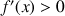 (le trinôme du second degré 3x2 + 2x +3 a un discriminant négatif, donc il garde un signe constant).
(le trinôme du second degré 3x2 + 2x +3 a un discriminant négatif, donc il garde un signe constant).
La fonction
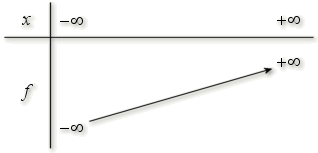
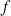 est donc une fonction strictement croissante sur R, de plus elle est continue sur R (puisqu'elle est dérivable).
est donc une fonction strictement croissante sur R, de plus elle est continue sur R (puisqu'elle est dérivable).
On obtient les limites de
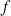 en utilisant les règles opératoires :
en utilisant les règles opératoires :
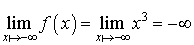 et
et 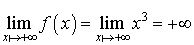 .
.
On peut alors donner le tableau de variations de
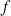 :
:
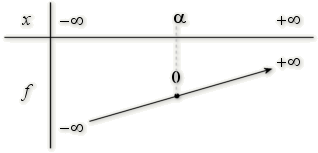
D'après le tableau de variations de
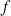 , l'équation
, l'équation
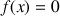 a une solution unique dans R :
a une solution unique dans R :
On peut remarquer que
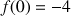 et
et
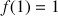 .
.
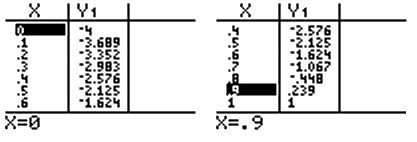
En utilisant le tableau de valeurs donné par une calculatrice :
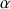 a pour valeur approchée 0,8 à 10-1 près (ou
a pour valeur approchée 0,8 à 10-1 près (ou
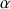 a pour valeur approchée 0,9 à 10-1 près).
a pour valeur approchée 0,9 à 10-1 près).
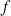 la fonction définie sur R par :
la fonction définie sur R par : ![]() .
.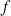 .
.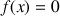 a une solution unique
a une solution unique
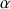 dans R.
dans R.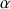 à
à
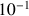 près.
près.