Enoncé
L'espace est rapporté au repère orthonormé 
. On considère les points 
, 
et 
. Soit
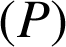le plan passant par
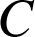et perpendiculaire à la droite
.
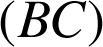Répondre par Vrai ou Faux aux affirmations suivantes :
2) Une équation de
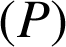est 
.
Résultat
Correction
Explications
On rappelle que , et et que
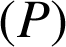est le plan passant par
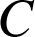et perpendiculaire à la droite
.
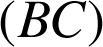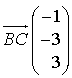est un vecteur normal à
.
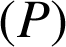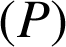est l'ensemble des points
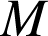tels que 
.
Si 
alors
Une équation de
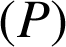est 
c'est-à-dire .
Autre façon :
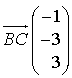est un vecteur normal à
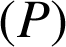donc
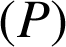a une équation de la forme 
, 
.
Les coordonnées de
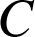vérifient cette égalité donc : 
, donc
.
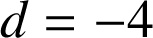Une équation de
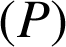est , c'est-à-dire .