Définition
Les vecteurs 
et 
sont orthogonaux si et seulement si leur produit scalaire est nul.
Propriété
Les vecteurs et sont orthogonaux si et seulement si leurs directions sont perpendiculaires ou si l'un des deux vecteurs est nul.
Vecteur normal à une droite :
C'est un vecteur non nul et orthogonal à un vecteur directeur de la droite.
Équation de droite :
Une droite
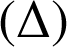a une équation de la forme 
si et seulement si le vecteur 
est un vecteur normal de
.
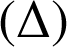Distance d'un point à une droite :
Soit
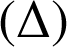la droite d'équation . Soit 
. La distance de
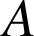à la droite
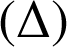est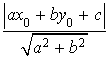 
.
