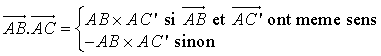Définition
Le plan est muni d'un repère orthonormal ![]() .
.
On considère deux vecteurs ![]() et
et ![]() .
.
Les définitions suivantes du produit scalaire de ces deux vecteurs sont équivalentes :
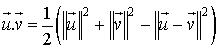 .
.Si
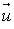 a pour coordonnées
a pour coordonnées 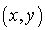 et
et 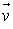 a pour coordonnées
a pour coordonnées 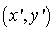 ,
, 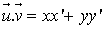 .
.Si
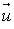 et
et 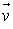 sont deux vecteurs non nuls,
sont deux vecteurs non nuls, 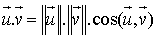 .
.Si
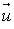 ou
ou 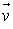 est nul,
est nul, 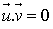 .
.Si
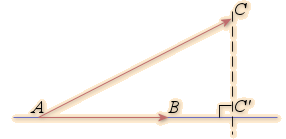
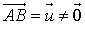 : si
: si
 est la projection orthogonale de
est la projection orthogonale de
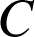 sur
sur 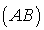 ,
, 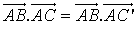 .
.Si
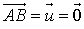 :
: 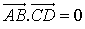 .
.
Remarque
Si ![]() ,
,