3) Le plan complexe est rapporté à un repère orthonormé direct 
.
On considère les points 
, 
, et 
et 
.
On désigne respectivement par
,
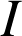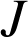et
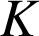les milieux de 
, 
et 
.
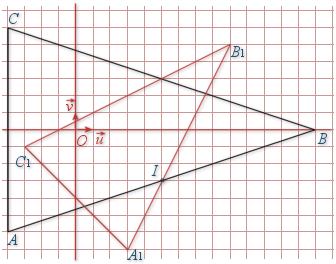
Soit
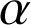l'angle de la similitude directe de centre
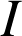qui transforme
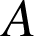en
.
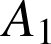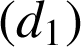est l' image de la droite
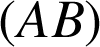par la rotation de centre
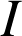et d'angle
.
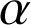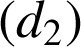est l' image de la droite
par la rotation de centre
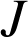et d'angle
.
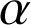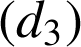est l' image de la droite
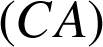par la rotation de centre
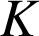et d'angle
.
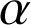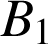est le point d'intersection de
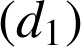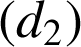et
, et
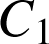celui de
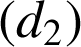et
.
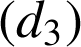